Information Flow Through a Network
Introduction
Modern financial markets operate very quickly due to algorithmic trading. Essentially, computers execute trades automatically based on information inputs and clever algorithms. All of this occurs very rapidly. The computers are so good at executing trades quickly, in fact, that the speed at which information moves from one city to another is actually a limiting factor. For example, if an announcement that impacts the financial markets is made in Washington, DC, traders in New York, NY will probably "hear" about it before those in, say, Seattle, WA.
Since information can travel no faster than the speed of light (in reality it travels much more slowly because of various processing that must be done along the way) we can compute a lower bound on the time it will take a particular piece of information released in one city to arrive in other cities. As you might expect, this problem involves flow through a network, and is therefore fairly simple to model in Neo4j (or any graph database, really).
Data Model
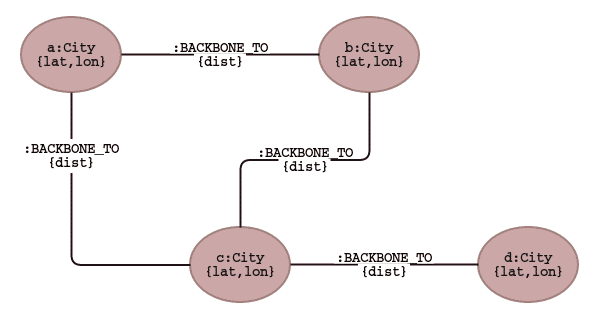
Our data model consists of a set of cities, each with a latitude and longitude, which we will use to compute distances (we could have entered the distances as data, but it was more fun to use Neo4j for this task, and in a more generalized case you might want the nodes to be able to move).
Each city is linked to one or more other cities by :BACKBONE_TO relationships.
This indicates that the two cities involved in the relationship have an Internet backbone running between them.
For this example, we mostly made up the backbones, although the backbones running to Tokyo are accurate given actual undersea cable topology.
Distance Computation
Before we can establish a lower bound on the time it takes information to flow between cities, we must determine the distance between cities that are linked by an Internet backbone. We assume that the cables connecting cities lie on great circles, in other words, that each cable lies on the shortest possible line between cities.
// Find the great circle distance from Tokyo to Seattle
MATCH (c1:City { name: "Tokyo" })
MATCH (c2:City { name: "Seattle" })
RETURN 2 * 6371 * asin(sqrt(haversin(radians(c1.lat - c2.lat)) + cos(radians(c1.lat)) * cos(radians(c2.lat)) * haversin(radians(c1.lon - c2.lon)))) AS DistanceIn our case we would like to record the distances between cities that are connected with an Internet backbone.
We can store this data on the :BACKBONE_TO edges.
Note that we don’t have to worry about double-computing because we have specified a relationship direction, so each distance will only be computed once.
If we left out the direction, each distance would be computed twice, although the end result would be exactly the same.
// Add distance to backbone edges
MATCH (c1:City)-[r:BACKBONE_TO]->(c2:City)
WITH 2 * 6371 * asin(sqrt(haversin(radians(c1.lat - c2.lat))+ cos(radians(c1.lat))* cos(radians(c2.lat))* haversin(radians(c1.lon - c2.lon)))) AS dist, r, c1, c2
SET r.dist = dist
RETURN c1.name, c2.name, r.distMapping Information Flow
Our next step is to find candidate paths from one city to another. Once we have these paths, we can compute the minimum amount of time it would take a piece of information to move along each path, and find the shortest route between them. First, we can find all unique, simple (no repeated cities) from one city to another. Here is example for Tokyo and Chicago:
// Find all unique, simple paths from one city to another
MATCH p=(:City { name: "Tokyo" })-[:BACKBONE_TO*]-(:City { name: "Chicago" })
WHERE all(c IN nodes(p) WHERE 1=size([m IN nodes(p) WHERE m=c]))
RETURN DISTINCT [ n IN nodes(p) | n.name] AS Path, length(p) AS LengthNext, we would like to find the shortest path, in terms of distance:
// Find the shortest distance path from one city to another
MATCH p=(:City { name: "Tokyo" })-[:BACKBONE_TO*]-(:City { name: "Chicago" })
WHERE all(c IN nodes(p) WHERE 1=size([m IN nodes(p) WHERE m=c]))
WITH reduce(s = 0, hop IN relationships(p) | s + hop.dist) AS distance, p
ORDER BY distance LIMIT 1
RETURN DISTINCT [n IN nodes(p) | n.name] AS Path, length(p) AS Length, distance AS DistanceThe next step is to change distance into an amount of time. We will assume that information travels between cities at the speed of light. As mentioned earlier this is not strictly true, but since we are looking for a lower bound on the time it takes information to move from one city to another, using the fastest possible speed for the information flow itself makes sense.
As an aside, we could make this model more complicated, and perhaps more accurate, by taking into account the processing time each each junction point along the way. When information arrives at a particular node in the network it must be routed to the next node along its path, this takes some non-zero amount of time. Therefore, we might actually want to minimize the distance information has to travel, subject to the constraint that each "hop" has a cost. In this case, we would tend to prefer less complicated paths, even if they are slightly longer.
We can compute the number of milliseconds it should take information to travel between cities using the query below. Note that we simply divide the distance by 300 to get milliseconds, since light travels at 300,000 kilometers per second.
// Find the shortest distance path from one city to another
MATCH p=(:City { name: "Tokyo" })-[:BACKBONE_TO*]-(:City { name: "Chicago" })
WHERE all(c IN nodes(p) WHERE 1=size([m IN nodes(p) WHERE m=c]))
WITH reduce(s = 0, hop IN relationships(p) | s + hop.dist) AS distance, p
ORDER BY distance LIMIT 1
RETURN DISTINCT [n IN nodes(p) | n.name] AS Path, length(p) AS Length, distance AS DistanceWe can then generalize this query to compute the time it would take information to travel between any pair of cities.
// Compute the minimum travel time between all pairs of cities
MATCH p=(c1:City)-[:BACKBONE_TO*]-(c2:City)
WHERE c1.name <> c2.name and all(c IN nodes(p) WHERE 1=size([m IN nodes(p) WHERE m=c]))
WITH reduce(s = 0, hop IN relationships(p) | s + hop.dist) AS distance, p, c1, c2
ORDER BY distance
RETURN c1.name AS `Start City`, c2.name AS `End City`, collect(distance / 300)[0] AS ms
ORDER BY c2.nameIs this page helpful?