Multidimensional graph metrics with Neo4j and Cypher

The goal of this Gist is to demonstrate the graph metrics collected in our paper Towards the characterization of realistic models: evaluation of multidisciplinary graph metrics.

Dataset

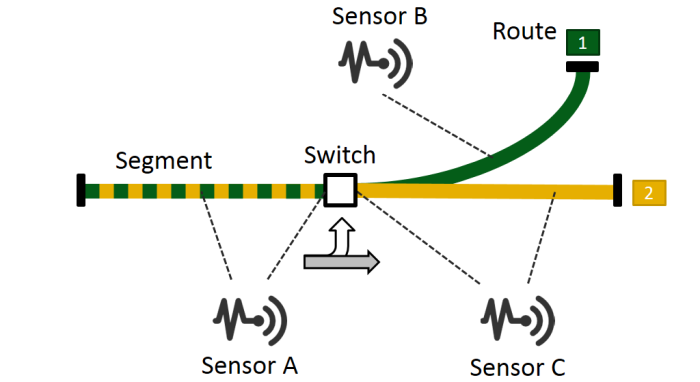
As an example, we use a simple railway network consisting of two Routes, three Segments, a Switch and three Sensors.

Figure 1. Railway network

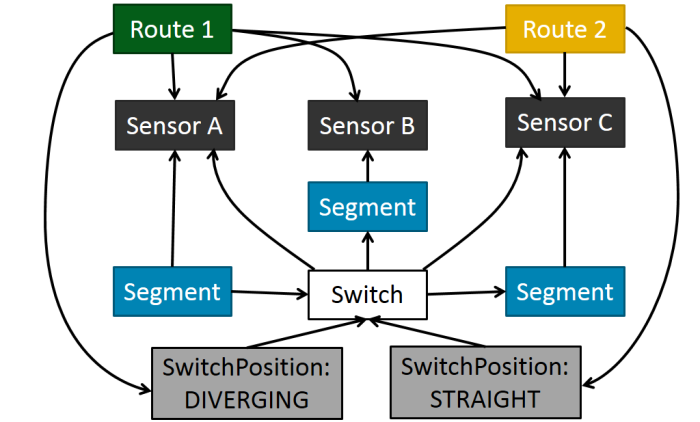
A possible graph representation of the example as a graph is this:

Figure 2. Railway graph

This short video demonstrates how the railway network is transformed to a graph.

The following query creates the graph (the query is automatically executed when loading the page).

CREATE
  // nodes
  (route1:Route {name:"Route1"}), (route2:Route {name:"Route2"}),
  (sensorA:Sensor {name:"SensorA"}), (sensorB:Sensor {name:"SensorB"}), (sensorC:Sensor {name:"SensorC"}),
  (segment1:Segment {name:"Segment1"}), (segment2: Segment {name:"Segment2"}), (segment3: Segment {name:"Segment3"}),
  (sw:Switch {name:"Switch"}),
  (swP1:SwitchPosition {name:"SwP1", position:"DIVERGING"}), (swP2:SwitchPosition {name:"SwP2", position:"STRAIGHT"}),
  // requires edges
  (route1)-[:requires]->(sensorA),
  (route1)-[:requires]->(sensorB),
  (route1)-[:requires]->(sensorC),
  (route2)-[:requires]->(sensorA),
  (route2)-[:requires]->(sensorC),
  // monitoredBy edges
  (segment1)-[:monitoredBy]->(sensorA),
  (sw)-[:monitoredBy]->(sensorA),
  (sw)-[:monitoredBy]->(sensorC),
  (segment2)-[:monitoredBy]->(sensorB),
  (segment3)-[:monitoredBy]->(sensorC),
  // connectsTo edges
  (segment1)-[:connectsTo]->(sw),
  (sw)-[:connectsTo]->(segment2),
  (sw)-[:connectsTo]->(segment3),
  // target edges
  (swP1)-[:target]->(sw),
  (swP2)-[:target]->(sw),
  // follows edges
  (route1)-[:follows]->(swP1),
  (route2)-[:follows]->(swP2)

In the following, we present the formal definitions of the metrics and evaluate them on the example graph using Cypher queries. For the details of the notation, see the paper.

One-dimensional metrics

Clustering coefficient

\(C(v) = \frac {\big| a, b \mid \mathit{Connected}(v, a) \land \mathit{Connected}(v, b) \land \mathit{Connected}(a, b) \big|} {\big| a, b \mid \mathit{Connected}(v, a) \land \mathit{Connected}(v, b) \big|}\)

MATCH (v)
OPTIONAL MATCH (v)-[r1]-(a1), (v)-[q1]-(b1)
WHERE a1 <> b1 AND r1 <> q1
WITH DISTINCT v, a1, b1
WITH DISTINCT v, toFloat(COUNT(a1)) AS possible

OPTIONAL MATCH (v)-[r2]-(a2)-[]-(b2)-[q2]-(v)
WHERE a2 <> b2 AND r2 <> q2
WITH DISTINCT v, a2, b2, possible
WHERE possible <> 0
WITH DISTINCT v, COUNT(a2) AS actual, possible
WITH v, actual/possible AS c
RETURN v.name, round(10^4 * toFloat(c))/10^4 AS c
ORDER BY v.name

Multidimensional metrics

Metrics interpreted on dimension-node pairs

Dimensional degree

\(\mathit{Degree}\left(v,d\right) = \left|\big\{ w \in V \mid \mathit{Connected}(v, w, d) \big\}\right|\)

Metrics interpreted on dimensions

Node dimension activity

\( \mathit{NDA}(d) = \big| \{ v \in V \mid \mathit{Active}(v,d) \} \big| \)

Node dimension connectivity

\( \mathit{NDC}(d) = \frac{\mathit{NDA}(d)}{|V|} \)

Edge dimension activity

\( \mathit{EDA}(d) = \big| \{ (v,w,d) \in E \mid v,w \in V \} \big| \)

Edge dimension connectivity

\( \mathit{EDC}(d) = \frac{\mathit{EDA}(d)}{|E|} \)

MATCH (v)
OPTIONAL MATCH (v)-[e]-()
WITH
  toFloat(COUNT(DISTINCT v)) AS numberOfVertices,
  toFloat(COUNT(DISTINCT e)) AS numberOfEdges

MATCH (v)-[e]-()
WITH
  DISTINCT type(e) AS dimension,
  COUNT(DISTINCT v) AS nda,
  COUNT(DISTINCT v)/numberOfVertices AS ndc,
  COUNT(DISTINCT e) AS eda,
  COUNT(DISTINCT e)/numberOfEdges AS edc
RETURN
  dimension,
  nda,
  round(10^4 * toFloat(ndc))/10^4 AS ndc,
  eda,
  round(10^4 * toFloat(edc))/10^4 AS edc

ORDER BY dimension

Metrics interpreted on nodes

Node activity

\( \mathit{NA}(v) = \big| \{ d \in D \mid \mathit{Active}(v, d) \} \big| \)

Multiplex participation coefficient

\( \mathit{MPC}(v) = \frac{|D|}{|D| - 1} \left[ 1 - \sum\limits_{d\in D}^{}{\left(\frac{\mathit{Degree}(v,d)}{\mathit{Degree}(v,D)}\right)^2} \right] \)

MATCH (v)-[e]-()
WITH
  toFloat(COUNT(e)) AS degreeTotal,
  toFloat(COUNT(DISTINCT type(e))) AS numberOfDimensions

MATCH (v)-[e]-()
WITH v, type(e) AS dimension, COUNT(e) AS dimensionalDegree, degreeTotal, numberOfDimensions
WITH v, COLLECT(dimensionalDegree) AS dimensionalDegrees, toFloat(SUM(dimensionalDegree)) AS vertexDegreeTotal, degreeTotal, numberOfDimensions
WITH
  v,
  numberOfDimensions / (numberOfDimensions-1) *
  (1 - REDUCE(deg = 0.0, x in dimensionalDegrees | deg + (x/vertexDegreeTotal)^2)) AS mpc
RETURN v.name, round(10^4 * toFloat(mpc))/10^4 AS mpc

ORDER BY v.name

Dimensional clustering coefficients

DC1 variant

\( \mathit{DC}_1(v) = \frac {\big| a, b \mid \mathit{Connected}(v, a, d_1) \land \mathit{Connected}(v, b, d_1) \land \mathit{Connected}(a, b, d_2) \land d_1 \neq d_2 \big|} {\big| a, b \mid \mathit{Connected}(v, a, d_1) \land \mathit{Connected}(v, b, d_1) \big|} \)

MATCH (v)
OPTIONAL MATCH (v)-[r1]-(a1), (v)-[q1]-(b1)
WHERE a1 <> b1 AND type(r1) = type(q1)
WITH DISTINCT v, a1, b1
WITH DISTINCT v, toFloat(COUNT(a1)) AS possible
WHERE possible <> 0

OPTIONAL MATCH (v)-[r2]-(a2)-[s2]-(b2)-[q2]-(v)
WHERE a2 <> b2 AND type(r2) = type(q2) AND type(r2) <> type(s2)
WITH DISTINCT v, a2, b2, possible
WITH DISTINCT v, COUNT(a2) AS actual, possible
WITH v, actual/possible AS dc1
RETURN v.name, round(10^4 * toFloat(dc1))/10^4 AS dc1
ORDER BY v.name

DC2 variant

\( \mathit{DC}_2(v) = \frac {\big| a, b \mid \mathit{Connected}(v, a, d_1) \land \mathit{Connected}(v, b, d_2) \land \mathit{Connected}(a, b, d_3) \land d_1 \neq d_2 \land d_2 \neq d_3 \land d_1 \neq d_3 \big|} {\big| a, b \mid \mathit{Connected}(v, a, d_1) \land \mathit{Connected}(v, b, d_2) \land d_1 \neq d_2 \big|)} \)

Metrics interpreted on dimension pairs

The node activity binary vector for each node v is defined as:

\( a_v = \left\{ a_v^{[1]},a_v^{[2]}, \dots, a_v^{[|D|]} \right\}, \text{where } a_v^{[d]} = \begin{cases} 1, & \text{if } \mathit{Active}(v,d),\\ 0, & \text{otherwise} \end{cases} \)

Using this vector, the pairwise multiplexity metric is:

\( Q(d_1, d_2) = \frac{1}{|V|} \sum_{v \in V} {a_v^{[d_1]} a_v^{[d_2]}} \)

MATCH (v)
WITH toFloat(COUNT(DISTINCT v)) AS numberOfVertices
MATCH (v)-[e]-()
WITH DISTINCT numberOfVertices,  type(e) AS d1
MATCH (v)-[e]-()
WITH DISTINCT numberOfVertices, d1, type(e) AS d2
OPTIONAL MATCH ()-[e1]-(v)-[e2]-()
WHERE type(e1) = d1 AND type(e2) = d2
WITH DISTINCT numberOfVertices, d1, d2, v
WITH DISTINCT d1, d2, COUNT(v)/numberOfVertices AS pairwise_multiplexity
RETURN d1, d2, round(10^4 * toFloat(pairwise_multiplexity))/10^4 AS pairwise_multiplexity
ORDER BY d1, d2

Is this page helpful?

GraphGists