Optimize Weakly Connected Component Projections

This article is intended for people using the Weakly Connected Components (WCC) algorithm from the Graph Data Science Neo4j library, whether you’re on-premises or in the cloud (AuraDS or Aura Graph Analytics), and for those who need to reduce the time and memory consumed by the projection.

Create a free graph database instance in Neo4j Aura

We’re going to present how to use the Neo4j Cypher query language to transform the graph topology inside the projections without changing the outcome of the WCC algorithm.

Instead of projecting nodes and relationships directly, we’ll use Cypher to send into the projection only the useful nodes and relationships.

The advantage is that for n nodes, there will be n-1 relationships at most, which means we can reduce the amount of memory and time needed for the projection, as well as for the execution of the WCC itself, and ultimately reduce costs.

Example

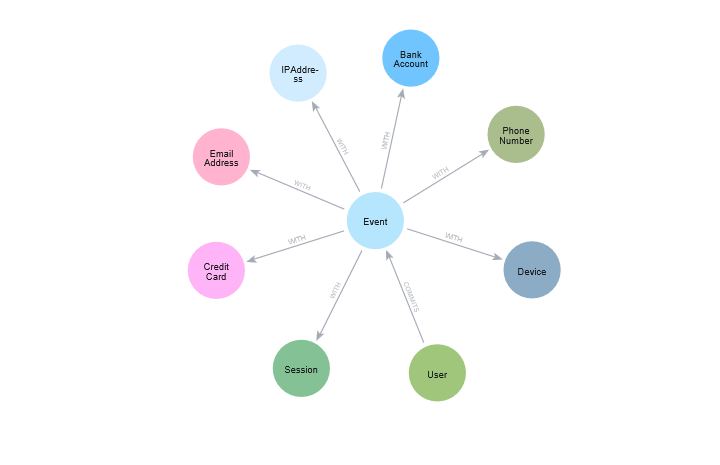
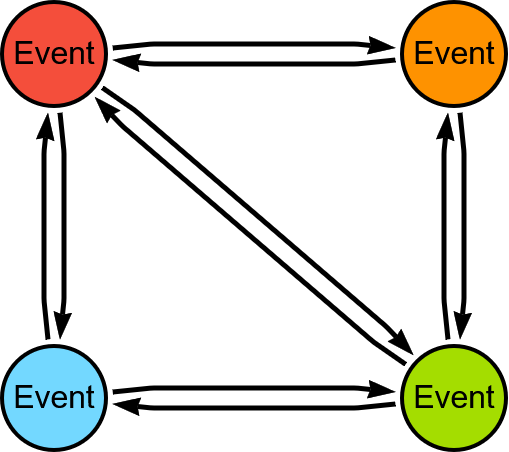
To illustrate, we used data from an article by Pierre Halftermeyer: Mastering Fraud Detection With Temporal Graph Modeling. The data model is shown below.

In our case, we want to compute the community of Event nodes by using the shared nodes between them, which are connected by WITH relationships. So we can simplify the data model as follows:

Default Version

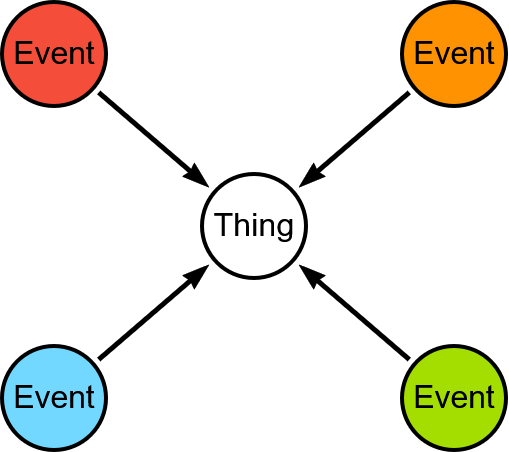
The first option projects the graph as stored in the database. The structure in memory will be identical to what’s in the database, which looks like the following image:

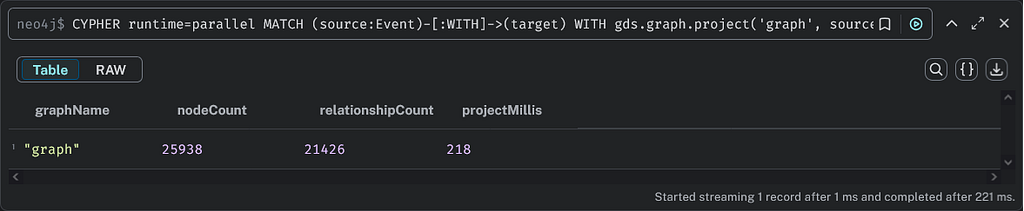
The following Cypher query projects the graph in memory:

CYPHER runtime=parallel
MATCH (source:Event)-[:WITH]->(target)
WITH gds.graph.project('graph', source, target) AS g
RETURN g.graphName AS graphName
  , g.nodeCount AS nodeCount
  , g.relationshipCount AS relationshipCount
  , g.projectMillis AS projectMillis

The parallel runtime was introduced with Neo4j 5.13.

We can then run the WCC algorithm, which gives 4,967 communities:

CALL gds.wcc.stream('graph')
YIELD nodeId, componentId
RETURN count(DISTINCT componentId) AS nb_components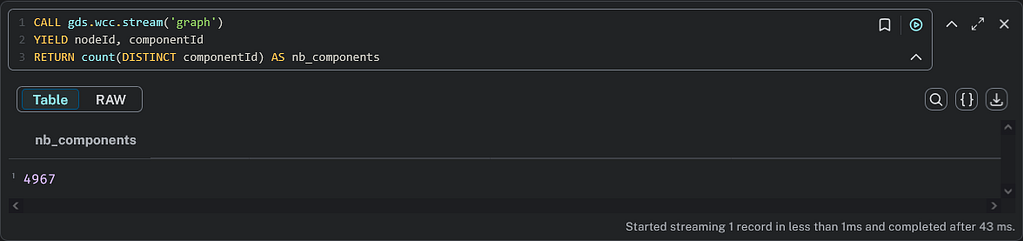

The disadvantage of this approach is that there are Thing nodes inside communities of Event nodes. Most of the time, it’s not necessary to give a community to these nodes, so we’ll see later how not to project them.

Improved Version

The second option projects Event nodes only, which means there won’t be Thing nodes inside the projection. The main advantage is that removing nodes will reduce the memory used by the projection. The topology will look like the following image:

The following Cypher query projects the graph in memory:

CYPHER runtime=parallel
MATCH (source:Event)-[:WITH]->(thing)
OPTIONAL MATCH (thing)<-[:WITH]-(target:Event)
WITH gds.graph.project('graph', source, target) AS g
RETURN g.graphName AS graphName
  , g.nodeCount AS nodeCount
  , g.relationshipCount AS relationshipCount
  , g.projectMillis AS projectMillis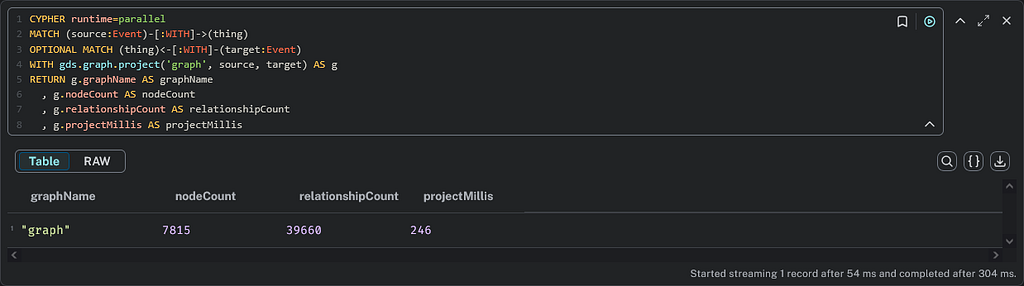

We can then run the WCC algorithm, which gives 4,967 communities.

However, we’ll have bidirectional relationships in the projection, which are useless for the execution of the WCC algorithm, so we can remove these with a little trick to get the following topology:

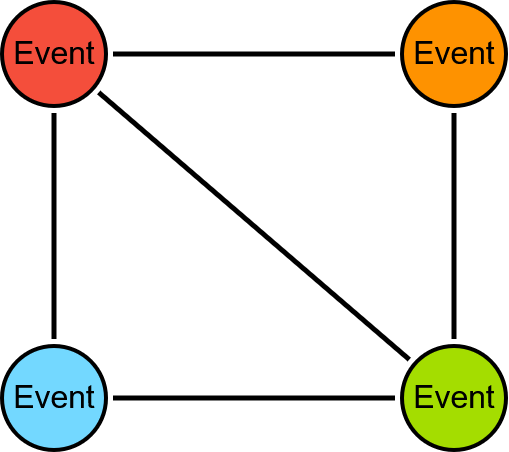
The following Cypher query projects the graph in memory:

CYPHER runtime=parallel
MATCH (source:Event)-[:WITH]->(thing)
OPTIONAL MATCH (thing)<-[:WITH]-(target:Event)
WHERE id(source) > id(target) // remove bidirectional relationships 
WITH gds.graph.project('graph', source, target) AS g
RETURN g.graphName AS graphName
  , g.nodeCount AS nodeCount
  , g.relationshipCount AS relationshipCount
  , g.projectMillis AS projectMillis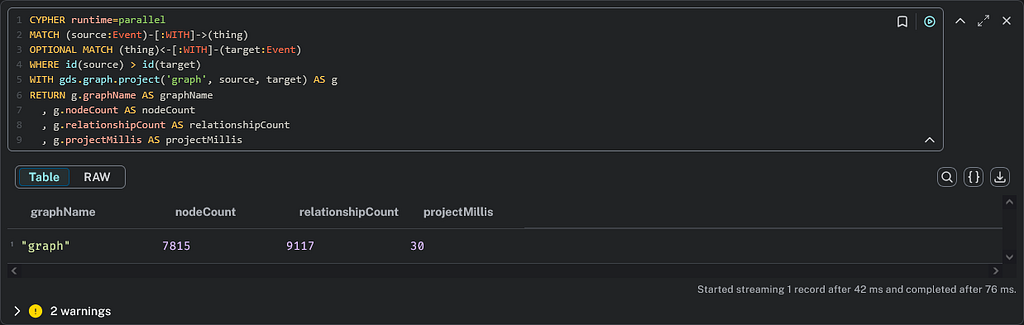

We can then run the WCC algorithm, which gives 4,967 communities.

NOTE: In the example, parallel relationships are loaded because some Event pairs share several Thing nodes, so before projecting, we could add a WITH DISTINCT source, target to keep only one relationship. We would then have 8,576 relationships and, of course, still 4,967 communities in output.

Optimized Version

This last option is an original idea of Pierre Halftermeyer’s, which allows us to keep only the nodes and relationships necessary for the execution of the WCC algorithm.

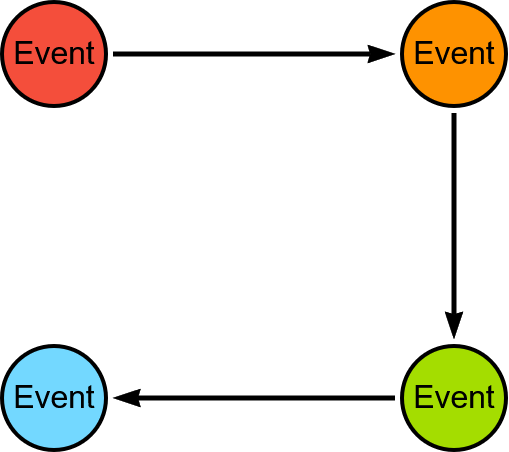
The result of WCC will be the same whether we connect all the nodes together as before or whether we keep only the minimum number of relationships to obtain a disjoint graph.

The in-memory graph topology will look like the following image:

The following Cypher query projects the graph in memory:

CYPHER runtime=parallel
MATCH (e:Event)-[:WITH]->(thing)
WITH thing, collect(e) AS events
UNWIND range(0, size(events)-1) AS ix
WITH events[ix] AS source, events[ix+1] AS target
WITH gds.graph.project('graph', source, target) AS g
RETURN g.graphName AS graphName
  , g.nodeCount AS nodeCount
  , g.relationshipCount AS relationshipCount
  , g.projectMillis AS projectMillis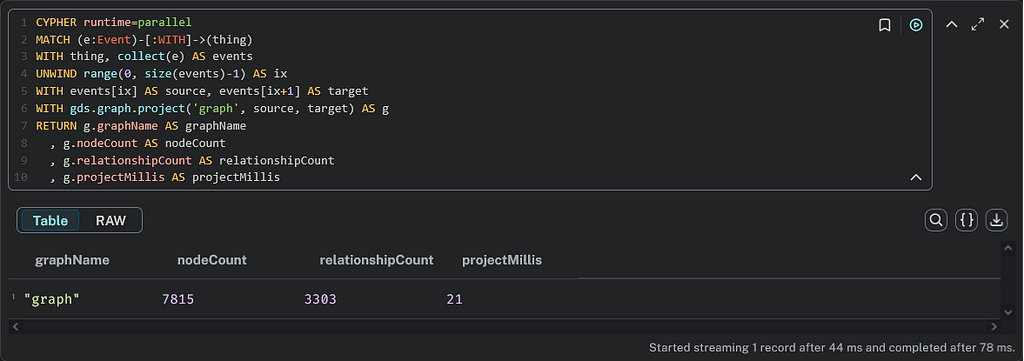

We can then run the WCC algorithm, which still gives 4,967 communities.

Comparison

We can see that the projection is faster with the optimized version, but the size of the projection stagnates, like the required memory to execute WCC. However, the larger the graph, the more interesting the savings will be — especially if you use Aura Graph Analytics.

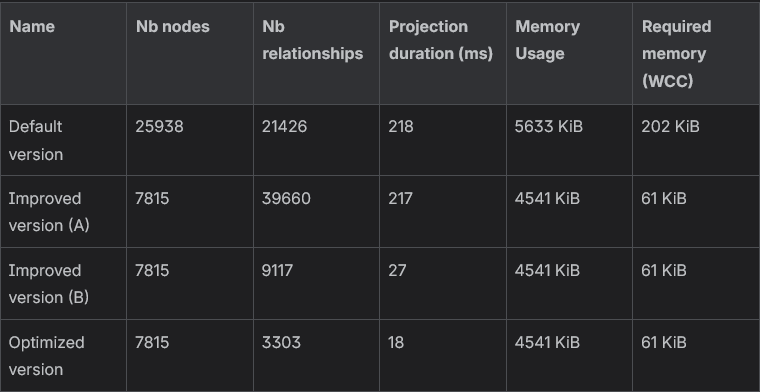
The memory usage of a projection can be computed thanks to the gds.graph.list() procedure.

Summary

We’ve presented several tips to optimize your WCC algorithm projections by playing with the graph topology while achieving the same result, including:

• Deleting intermediate nodes
• Deleting bidirectional relationships
• Building the most useful relationships between projected nodes

Now you have a way to optimize your WCC projections in time and in space!

Resources

• Neo4j Graph Data Science
• Neo4j Cypher Query Language
• Neo4j Cypher Manual

---

Optimize Weakly Connected Components Projections was originally published in Neo4j Developer Blog on Medium, where people are continuing the conversation by highlighting and responding to this story.