Create a free graph database instance in Neo4j AuraDB
In this post, I’ll show you various problems where the solution is a path that needs to double-back on itself, or that needs to repeat cycles, and how you can use the new REPEATABLE ELEMENTS match mode to do this.
Until the new REPEATABLE ELEMENTS match mode was introduced in Cypher 25*, path finding in Neo4j followed the rule that relationships never appear more than once for a given match. With the new REPEATABLE ELEMENTS match mode, users can specify that matches are allowed to return the same relationship more than once.
For most use cases, it makes more sense to follow the default match mode: DIFFERENT RELATIONSHIPS. Finding out whether two things are connected, and how they’re connected, doesn’t require backtracking or repeatedly following a cycle. That will remain the default match mode and the behavior you get if you leave your queries unchanged.
But there are cases where it makes sense to backtrack or repeat cycles:
- Optimal path finding with constraints
- Paths that need to visit every node or every relationship in a graph
- Finding peers reachable via a common ancestor
- Stateful processes or workflows
The following examples will demonstrate some of those uses, and hopefully spark ideas on how REPEATABLE ELEMENTS can be useful.
* Available in Neo4j Aura since June 2025 and Neo4j self-managed since release 2025.06
A Quick Detour for a Gas Station — Optimal Pathfinding With Constraints
Finding the optimal path between two nodes normally excludes revisiting any nodes (and relationships), as that would necessarily make the route longer than one that didn’t. But revisiting nodes might make sense if the route had a constraint — for example, finding the shortest journey from A to B with a gas station on the way.
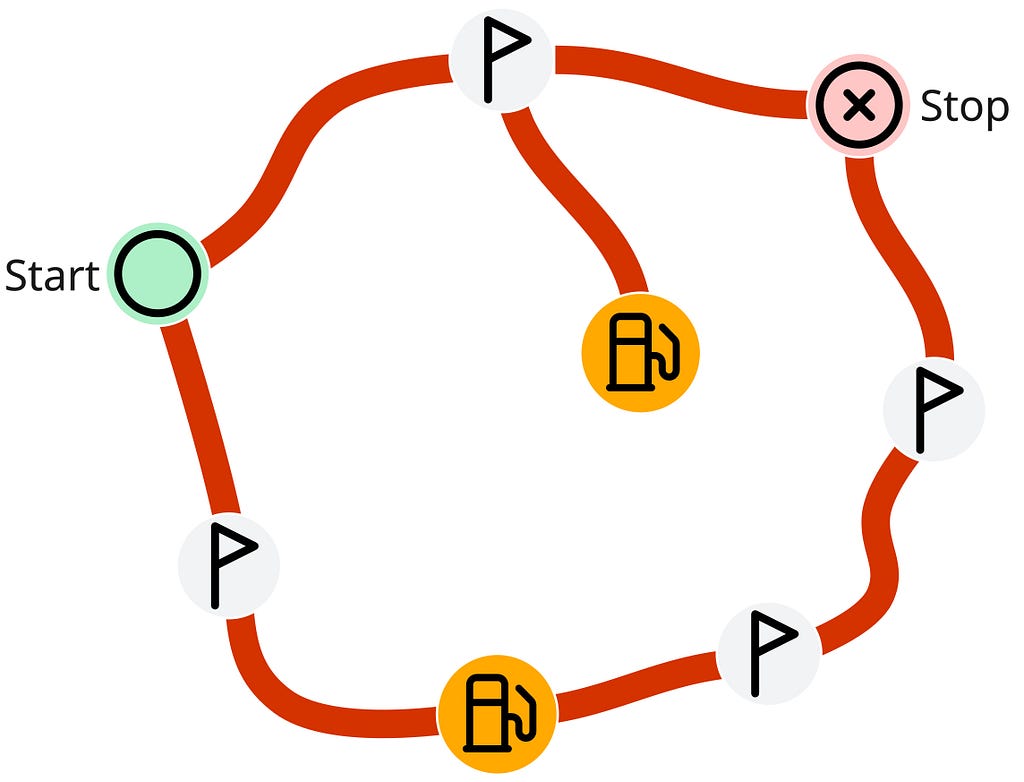
To illustrate with a simple example, consider a graph with a (:Start) node and a (:Stop) node connected by two direct routes. One route includes a gas station on the way; the other takes a detour to reach a gas station.
CREATE (n6:Waypoint)<-[:ROAD]-(:Waypoint)<-[:ROAD]-(:GasStation)<-[:ROAD]-
(:Waypoint)<-[:ROAD]-(:Start)-[:ROAD]->(n1:Waypoint)-[:ROAD]->
(:Stop)<-[:ROAD]-(n6), (n1)-[:ROAD]->(:GasStation)Using Cypher’s default match mode, which would disallow the detour, forces us to take the long way:
MATCH route = SHORTEST 1 (:Start)--+(:GasStation)--+(:Stop)
RETURN length(route) AS length
+--------+
| length |
+--------+
| 5 |
+--------+If we use REPEATABLE ELEMENTS, the gas station is accessible via the detour, and we save ourselves one hop:
MATCH REPEATABLE ELEMENTS
route = ANY SHORTEST (:Start)--{,100}(:GasStation)--{,100}(:Stop)
RETURN length(route) AS length
+--------+
| length |
+--------+
| 4 |
+--------+
1 rowWe had to add an upper limit to the number of repetitions (arbitrarily set to 100 in the example) to guarantee a finite number of results. Because REPEATABLE ELEMENTS has unlimited backtracking, it has the potential to generate an infinite number of solutions. In theory, ANY SHORTEST should only return a single match, but we still needed to add a limit, as it is possible to add an unsatisfiable WHERE clause, which would lead to a search that never halts.
Doctor’s Rounds
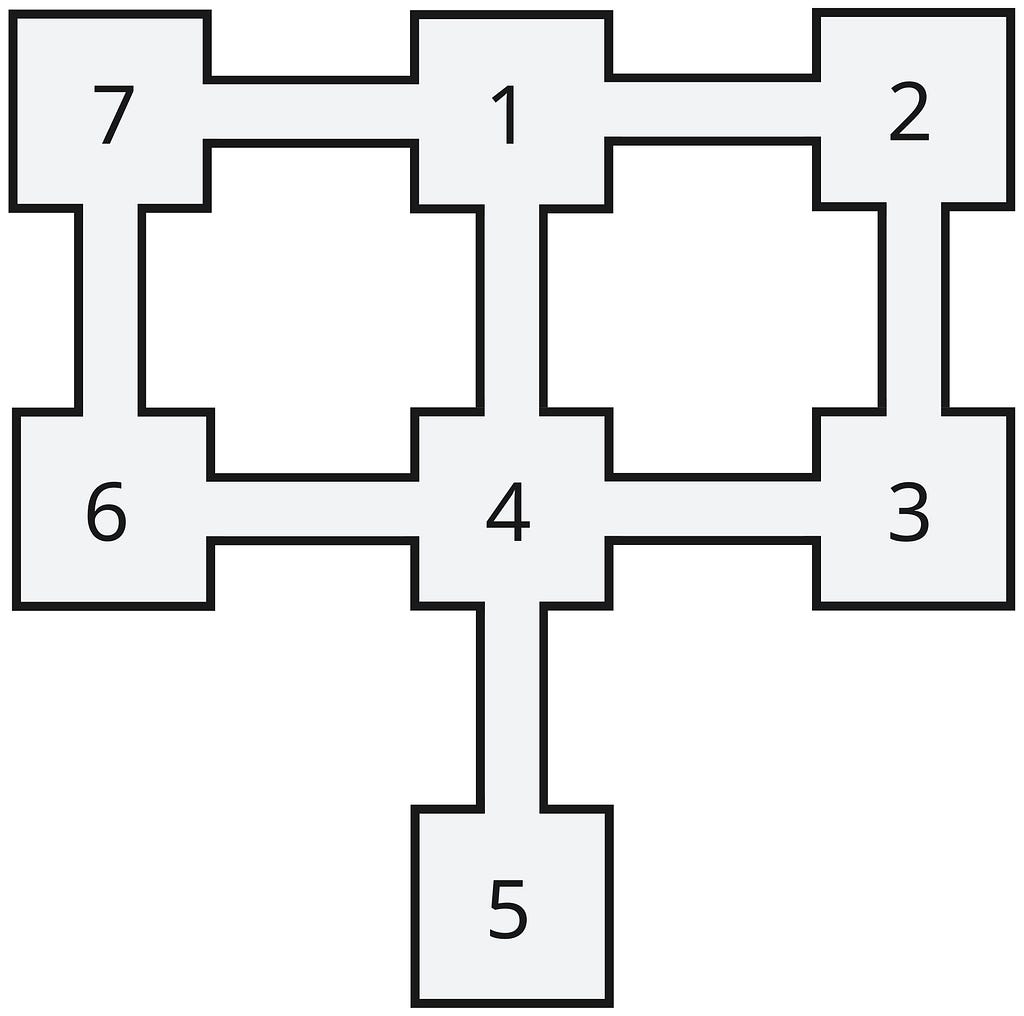
One area where paths may go over relationships multiple times is in the modeling of real-world movement. For example, imagine a doctor needing to visit every ward on a floor at least once, starting and finishing their rounds in ward 1, and wanting to optimize the route by minimizing the number of corridors and wards they pass through.
Here’s a simple topology of wards represented in a graph, with the wards as nodes and the corridors connecting the wards as relationships:
CREATE (n7:Ward {id: 7})-[:CORRIDOR]->(n1:Ward {id: 1})-[:CORRIDOR]->
(n4:Ward {id: 4})-[:CORRIDOR]->(:Ward {id: 6})-[:CORRIDOR]->(n7),
(n1)-[:CORRIDOR]->(:Ward {id: 2})-[:CORRIDOR]->
(:Ward {id: 3})-[:CORRIDOR]->(n4)-[:CORRIDOR]->(:Ward {id: 5})We can see just by inspection that it isn’t possible to visit every ward exactly once, and any optimal route will visit some wards more than once. To find the optimal paths, we can use ALL SHORTEST, which will return all paths that have the minimum number of hops:
LET wards = COLLECT { MATCH (n:Ward) RETURN n }
MATCH ALL SHORTEST
(p = (start {id: 1})--{ ,11}(start)
WHERE all(ward IN wards WHERE ward IN nodes(p)))
WITH length(p) AS pathLength, collect(p) AS paths ORDER BY pathLength LIMIT 1
UNWIND paths AS p
RETURN [n IN nodes(p) | n.id] AS `Doctor's rounds`But as we haven’t specified a particular match mode here, we get the default match mode DIFFERENT RELATIONSHIPS, and get no results due to the fact that there is no path that doesn’t require going down the same corridor more than once:
+-----------------+
| Doctor's rounds |
+-----------------+
+-----------------+
0 rowsWe can enable repeated traversals of corridors with the REPEATABLE ELEMENTS match mode:
LET wards = COLLECT { MATCH (n:Ward) RETURN n }
MATCH REPEATABLE ELEMENTS ALL SHORTEST
(p = (start {id: 1})--{ ,11}(start)
WHERE all(ward IN wards WHERE ward IN nodes(p)))
WITH length(p) AS pathLength, collect(p) AS paths ORDER BY pathLength LIMIT 1
UNWIND paths AS p
RETURN [n IN nodes(p) | n.id] AS `Doctor's rounds`Allowing the re-traversal of corridors, we find two optimal routes, both with room 4 being visited twice (1 is visited twice by being at the start and end):
+-----------------------------+
| Doctor's rounds |
+-----------------------------+
| [1, 7, 6, 4, 5, 4, 3, 2, 1] |
| [1, 2, 3, 4, 5, 4, 6, 7, 1] |
+-----------------------------+
2 rowsHere’s one of the solutions visualized:
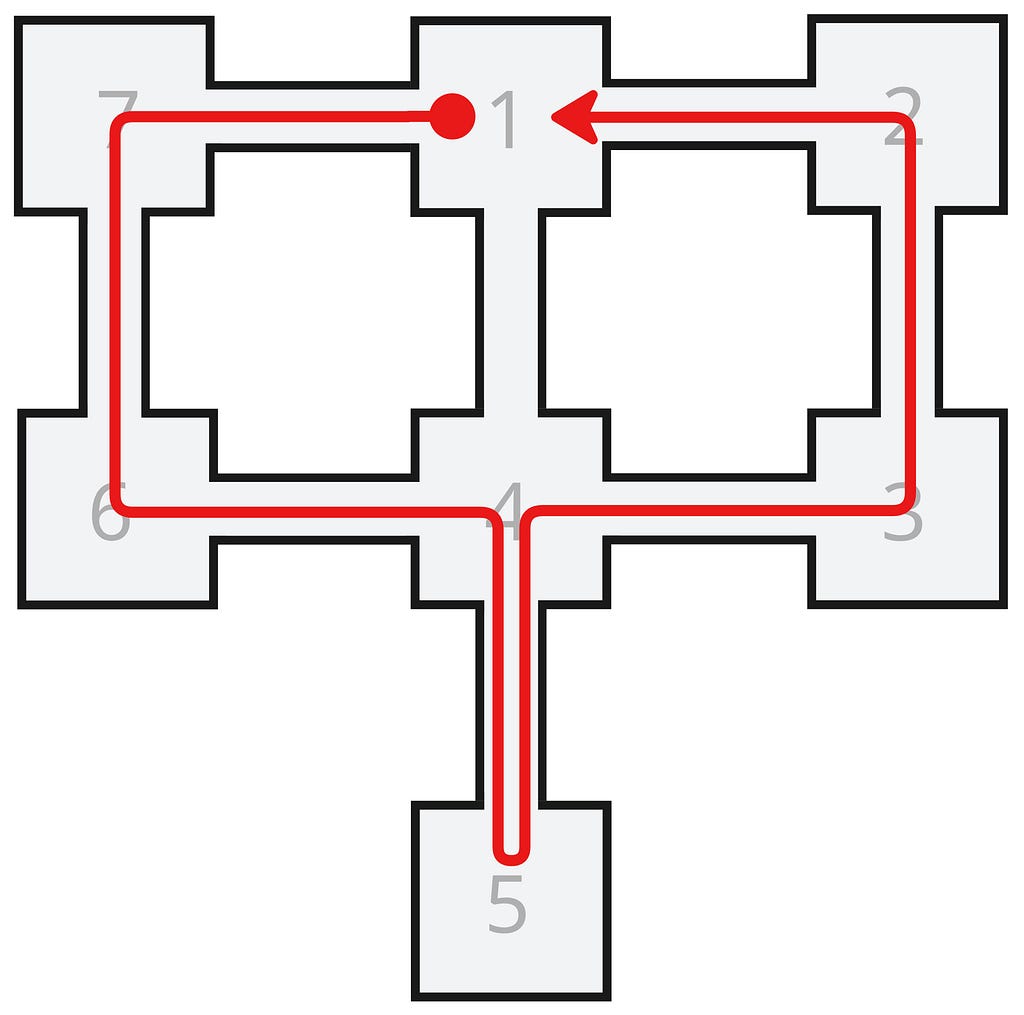
With the simplicity of the layout, these two solutions are hardly surprising (each path is just the reverse of the other), but it illustrates the point. Later, we’ll look at a more interesting covering path example: Pac-Man.
Peer-to-Peer Reachability Across a Family Tree
In a hierarchical graph, the relationships are primarily between parent-child nodes. For instance, in a family tree, you’d only see MOTHER and FATHER relationships, and not GRANDMOTHER or GRANDFATHER relationships (nth order relationships are implicit).
The following example shows a small family tree of depth 2 with some half-siblings:

CREATE ({name: "Mia"})<-[:MOTHER]-(n1 {name: "Amelia"})-[:FATHER]->
({name: "James"}), (n1)<-[:MOTHER]-({name: "Arthur"})-[:FATHER]->
(n6 {name: "Theo"})<-[:FATHER]-({name: "Felix"})-[:MOTHER]->
(n1)<-[:MOTHER]-({name: "Kai"})-[:FATHER]->
(n5 {name: "Oliver"})-[:FATHER]->({name: "Liam"}),
({name: "Asher"})<-[:FATHER]-(n6)-[:MOTHER]->({name: "Charlotte"}),
(n5)-[:MOTHER]->({name: "Olivia"})One implication of this type of graph is that relationships between siblings via ancestors that are more than a level away are discoverable only by re-traversing relationships. Here, we can only see that Kai shares the grandparent Mia with Felix via this path:
({name: "Kai"})-[:MOTHER]->({name: "Amelia"})-[:MOTHER]->
({name: "Mia"})<-[:MOTHER]-({name: "Amelia"})<-[:MOTHER]-({name: "Felix"})How many grandparents do these two people have in common? Answering that requires re-traversing a parent-to-grandparent relationship. If we attempt to match these paths in a single pattern under the default DIFFERENT RELATIONSHIPS match mode, no results will be returned:
MATCH (kidA)-[:MOTHER|FATHER]->{2}(grandparent)<-[:MOTHER|FATHER]-{2}(kidB)
WHERE kidA < kidB
RETURN kidA.name, kidB.name,
count(DISTINCT grandparent) AS `Number of Grandparents in Common`
+----------------------------------------------------------+
| kidA.name | kidB.name | Number of Grandparents in Common |
+----------------------------------------------------------+
+----------------------------------------------------------+
0 rowsBecause relationship uniqueness is enforced only within a single MATCH, one solution is to split the path matching into two separate instances of MATCH:
MATCH (kidA)-[:MOTHER|FATHER]->{2}(grandparent)
MATCH (grandparent)<-[:MOTHER|FATHER]-{2}(kidB)
WHERE kidA < kidB
RETURN kidA.name, kidB.name,
count(DISTINCT grandparent) AS `Number of Grandparents in Common`
+----------------------------------------------------------+
| kidA.name | kidB.name | Number of Grandparents in Common |
+----------------------------------------------------------+
| "Arthur" | "Felix" | 4 |
| "Arthur" | "Kai" | 2 |
| "Felix" | "Kai" | 2 |
+----------------------------------------------------------+
3 rowsInstead, we can use REPEATABLE ELEMENTS to match in a single pattern:
MATCH REPEATABLE ELEMENTS
(kidA)-[:MOTHER|FATHER]->{2}(grandparent)<-[:MOTHER|FATHER]-{2}(kidB)
WHERE kidA < kidB
RETURN kidA.name, kidB.name,
count(DISTINCT grandparent) AS `Number of Grandparents in Common`
+----------------------------------------------------------+
| kidA.name | kidB.name | Number of Grandparents in Common |
+----------------------------------------------------------+
| "Arthur" | "Felix" | 4 |
| "Arthur" | "Kai" | 2 |
| "Felix" | "Kai" | 2 |
+----------------------------------------------------------+
3 rowsThe advantage here is minimal. But in cases where there are constraints that span the path and would allow expansions to be pruned — for example, requiring the total length of the path to be between 1 and 10 — then it becomes more efficient to solve as a single path.
Grammar Generator
In this example, we define a tiny language representing Cypher’s path patterns. In this language, we’re only allowed empty node patterns () and the abbreviated relationship patterns -->, <--, and --. For example, these patterns are in this language:
()
()-->()
()--()<--()-->()These are fixed-length path patterns without any variable declarations, label expressions, or predicates.
The following graph represents a generator for this tiny language:

CREATE (:Start)-[:R]->(leftParen {symbol: "("})-[:R]->(end:End {symbol: ")"}),
(end)-[:R]->({symbol: "--"})-[:R]->(leftParen),
(end)-[:R]->({symbol: "-->"})-[:R]->(leftParen),
(end)-[:R]->({symbol: "<--"})-[:R]->(leftParen)Every valid path pattern must be an alternating sequence of node and relationship patterns. They must also begin and end with a node pattern, and the first and last letters of any word in this tiny path pattern language are ( and ), respectively. We mark these letters with the labels Start and End.
To generate valid words in this language, we can use a variable-length path pattern that anchors on the Start and End nodes. The following path pattern would match path patterns of up to nine symbols:
(:Start) (()-->(n)){,9} (:End)If we use the default Cypher match mode, we find that we only get one word:
MATCH p = (:Start) (()-->(n)){,9}(:End)
LET letters = [node IN n | node.symbol]
RETURN reduce(acc = "", l IN letters | acc + l) AS word
+------+
| word |
+------+
| "()" |
+------+
1 rowThis is because any paths longer than the empty node pattern () would require repeating the relationship joining the ( and ) symbols.
By allowing relationship repetition with REPEATABLE ELEMENTS, however, we get all possible path patterns that are nine symbols or fewer:
MATCH REPEATABLE ELEMENTS p = (:Start)-->{,9}(:End)
WITH [n IN nodes(p) | n.symbol] AS letters
RETURN reduce(acc = "", l IN letters | acc + l) AS word
+----------------+
| word |
+----------------+
| "()" |
| "()--()" |
| "()-->()" |
| "()<--()" |
| "()--()--()" |
| "()--()-->()" |
| "()--()<--()" |
| "()-->()--()" |
| "()-->()-->()" |
| "()-->()<--()" |
| "()<--()--()" |
| "()<--()-->()" |
| "()<--()<--()" |
+----------------+
13 rowsThe Pac-Man Pellet Path Problem
WARNING: The Cypher at the end of the example uses some complex trickery. We don’t recommend hard-to-read queries. The point is just to show that the problem can be broken up into small, tractable pieces, and for simplicity, we did it all in Cypher.
As mentioned, variable-length path patterns need to have finite upper bounds on their length. This is due to the potentially infinite number of paths once backtracking and repeated cycles are allowed. Looking back at the example of the doctor’s rounds, because the graph consisted of seven nodes and eight relationships, the search space is very small. What happens if we increase the search space? To consider this, instead of a problem of visiting every node, we’ll look at the visiting-every-relationship problem. This is related to the Eulerian path problem — finding a path that visits every relationship in a graph once — which, in the form of the Seven Bridges of Königsberg, was the foundational problem in graph theory (see the documentation on match modes for more).
The game of Pac-Man, with some simplifications, can be viewed as a covering path problem. If we simplify the game down to one of just eating the dots and ignore the problem of avoiding the ghosts, the maze can be modeled as a set of relationships representing the corridors with dots and a set of nodes as the junctions between those corridors. If Pac-Man visits every relationship at least once, every dot is eaten, and the level is completed.
In this model, we represent the starting point with the label Start, marked in yellow below. Empty corridors (except at the starting point) are excluded, junction numbers are shown.

CREATE
(n5:Dot {junction: 5})-[:CORRIDOR]->(n6:Dot {junction: 6})<-[:CORRIDOR]-
(n1:Dot {junction: 1})-[:CORRIDOR]->(n3:Dot {junction: 3})-[:CORRIDOR]->
(n4:Dot {junction: 4})-[:CORRIDOR]->(n5)-[:CORRIDOR]->(:Dot {junction: 12}),
(n1)-[:CORRIDOR]->(n4)-[:CORRIDOR]->(n11:Dot {junction: 11})-[:CORRIDOR]->
(n17:Dot {junction: 17}), (n3)-[:CORRIDOR]->(n11),
(n20:Dot {junction: 20})<-[:CORRIDOR]-(n14:Dot {junction: 14})<-[:CORRIDOR]-
(n9:Dot {junction: 9})-[:CORRIDOR]->(n10:Dot {junction: 10})<-[:CORRIDOR]-
(n2:Dot {junction: 2})-[:CORRIDOR]->(n7:Dot {junction: 7})-[:CORRIDOR]->
(n8:Dot {junction: 8})-[:CORRIDOR]->(n13:Dot {junction: 13}),
(n6)-[:CORRIDOR]->(n7), (n8)-[:CORRIDOR]->(n9)<-[:CORRIDOR]-(n2),
(n10)-[:CORRIDOR]->(n14), (n25:Dot {junction: 25})<-[:CORRIDOR]-
(n24:Dot {junction: 24})<-[:CORRIDOR]-(n20)-[:CORRIDOR]->
(n28:Dot {junction: 28})<-[:CORRIDOR]-(n26:Dot {junction: 26})<-[:CORRIDOR]-
(n25)-[:CORRIDOR]->(n30:Dot {junction: 30})<-[:CORRIDOR]-
(n29:Dot {junction: 29})<-[:CORRIDOR]-(n27:Dot {junction: 27}),
(n17)-[:CORRIDOR]->(n21:Dot {junction: 21})-[:CORRIDOR]->
(n22:Dot {junction: 22})-[:CORRIDOR]->(n23:Dot:Start {junction: 23})<-[:CORRIDOR]-
(n17)-[:CORRIDOR]->(n27)<-[:CORRIDOR]-(n21),
(n20)-[:CORRIDOR]->(n26), (n28)-[:CORRIDOR]->(n30),
(n22)-[:CORRIDOR]->(n29), (n23)-[:CORRIDOR]->(n24)If a Eulerian path existed (which would solve the problem), every node except two would be connected to an even number of relationships. For a Eulerian circuit, which starts and ends at the same node, all nodes have to be connected to an even number of relationships. But we can see that neither is possible on the Pac-Man board:
MATCH (n) WHERE COUNT { (n)--() } % 2 = 1
RETURN count(*) AS numWithOddDegree;
+------------------+
| numWithOddDegree |
+------------------+
| 22 |
+------------------+
1 rowSo any optimal path that Pac-Man takes will need to re-traverse some relationships. We need to use REPEATABLE ELEMENTS.
A first attempt:
LET corridors = COLLECT { MATCH ()-[r]->() RETURN r }
MATCH REPEATABLE ELEMENTS ALL SHORTEST
(p = (:Start)--{,30}()
WHERE all(corridor IN corridors WHERE corridor IN relationships(p)))
RETURN pBut before you try this — don’t. It is unlikely to ever return any results, and depending on your database configuration, may well abort due to insufficient memory being allocated. So we see that in scaling up a path-covering problem from a doctor’s route covering seven wards and hallways hallways to Pac-Man covering 39 corridors and 26 junctions, the number of possible paths to explore has exploded.
All is not lost. Depending on the topology of a problem, it may be possible to turn large problems into a number of smaller, more tractable path-finding problems that can then be connected to produce the overall solution. Fortunately, this is the case for the Pac-Man board.
Dividing the board into four zones should produce reasonably sized subgraphs. The different zones are identified by colorings on the relationships (and the types YELLOW, RED, BLUE, and GREEN in the data).

CREATE
(n5:Dot {junction: 5, x: 8, y: 4})-[:YELLOW]->
(n6:Dot {junction: 6, x: 11, y: 4})<-[:YELLOW]-
(n1:Dot {junction: 1, x: 5, y: 0})-[:YELLOW]->
(n3:Dot {junction: 3, x: 0, y: 4})-[:YELLOW]->
(n4:Dot {junction: 4, x: 5, y: 4})-[:YELLOW]->
(n5)-[:YELLOW]->(n12:Dot {junction: 12, x: 11, y: 7}),
(n1)-[:YELLOW]->(n4)-[:YELLOW]->
(n11:Dot {junction: 11, x: 5, y: 7})-[:BLUE]->
(n16:Dot {junction: 17, x: 5, y: 19}),
(n3)-[:YELLOW]->(n11),
(n20:Dot {junction: 20, x: 20, y: 19})<-[:RED]-
(n14:Dot {junction: 14, x: 20, y: 7})<-[:RED]-
(n9:Dot {junction: 9, x: 20, y: 4})-[:RED]->
(n10:Dot {junction: 10, x: 25, y: 4})<-[:RED]-
(n2:Dot {junction: 2, x: 20, y: 0})-[:RED]->
(n7:Dot {junction: 7, x: 14, y: 4})-[:RED]->
(n8:Dot {junction: 8, x: 17, y: 4})-[:RED]->
(:Dot {junction: 13, x: 14, y: 7}),
(n6)-[:YELLOW]->(n7),
(n8)-[:RED]->(n9)<-[:RED]-(n2),
(n10)-[:RED]->(n14),
(n25:Dot {junction: 25, x: 17, y: 22})<-[:GREEN]-
(n24:Dot {junction: 24, x: 14, y: 22})<-[:GREEN]-
(n20)-[:GREEN]->
(n28:Dot {junction: 28, x: 23, y: 25})<-[:GREEN]-
(n26:Dot {junction: 26, x: 20, y: 22})<-[:GREEN]-
(n25)-[:GREEN]->
(n30:Dot {junction: 30, x: 14, y: 28})<-[:GREEN]-
(n29:Dot {junction: 29, x: 11, y: 28})<-[:BLUE]-
(n27:Dot {junction: 27, x: 2, y: 25}),
(n16)-[:BLUE]->
(n21:Dot {junction: 21, x: 5, y: 22})-[:BLUE]->
(n22:Dot {junction: 22, x: 8, y: 22})-[:BLUE]->
(n23:Dot:Start {junction: 23, x: 11, y: 22})<-[:BLUE]-
(n16)-[:BLUE]->(n27)<-[:BLUE]-(n21),
(n20)-[:GREEN]->(n26), (n28)-[:GREEN]->(n30),
(n22)-[:BLUE]->(n29), (n23)-[:GREEN]->(n24)For this second version of the model, we introduce the node properties x and y, which represent coordinates on a grid. The grid is scaled so that the Manhattan distance between adjacent junctions will correspond to the distances in the actual Pac-Man game. With Pac-Man traveling at a constant speed, the distances will be proportional to the time taken to travel between junctions (and proportional to the number of dots). We’ll use these distances to calculate the optimal path in terms of distance and time taken.
To find covering paths within each zone that will connect together at the right junctions entirely in Cypher requires some gymnastics. The main tricks are (1) using reduce() to iterate over the four zones, and (2) hacking COLLECT { } to act as a scalar subquery. More detailed explanations as to what each part does are in the inline comments:
// We need to iterate once for each "zone" in our maze. The zones are defined
// by the relationship types (YELLOW, RED, GREEN, BLUE). This line dynamically
// counts how many distinct relationship types exist in the entire graph and
// uses the LET statement to assign the value to numZones. LET is another new
// Cypher 25 feature.
LET numZones = COUNT { CALL db.relationshipTypes() YIELD relationshipType }
// This fins Pac-Man's starting junction, which is explicitly marked with
// the :Start label. This node will be the entry point for solving the very
// first zone.
MATCH (start:Start)
// The reduce() function iterates a number of time, buildingh up a result
// in the accumulator pathAcc. Here, we will iterate numZones times, solving
// one zone in each iteration.
RETURN
reduce(
// Here we set the starting value of our accumulator, a map containing
// everything we need to track our progress through the maze:
//
// start: The node where we begin the current iteration. Initially,
// this is Pac-Man's starting node in the whole maze. After
// solving a zone, this will be updated to the exit node of
// the zone.
//
// seq: The list of paths for each zone that we are building up.
// After each iteration, we append the path for the current
// zone. It starts empty.
//
// visited: A list of zones (by color/type) that we have already cleared.
// It helps pick the next unvisited zone to link the path to.
pathAcc = {
start: start,
seq: [],
visited: []
},
// This iterates over the number of zones.
i IN range(1, numZones) |
// ------ THE "SUBQUERY-IN-A-LOOP" TRICK ------
// We need to perform several complex steps (find zone, find exits, find
// path) to calculate the next state of pathAcc. Cypher's reduce expects
// a simple expression. The COLLECT { ... }[0] pattern is a hack
// (just a little bit 🤏) allowing us to execute a multi-statement
// subquery and have it return a single value (in this case, the updated
// pathAcc map).
COLLECT {
// ------ IDENTIFY THE CURRENT ZONE ------
// From our current location (pathAcc.start), find all connecting
// relationship types that we haven't visited yet. This determines
// which zone we are about to solve. For the first iteration, this will
// be the zone connected to the :Start node.
MATCH (s)-[r]-()
WHERE
s = pathAcc.start AND
NOT type(r) IN pathAcc.visited
WITH DISTINCT type(r) AS zone
// ------ COLLECT ALL RELATIONSHIPS IN THE ZONE ------
// To clear a zone of pellets, we must traverse every relationship
// in it. We create a list of all relationships with COLLECT { } and
// assign to the variable rels.
LET rels = COLLECT { MATCH ()-[rel:$(zone)]->() RETURN rel }
// ------ FIND THE EXIT JUNCTIONS FOR THE ZONE ------
// An exit point is a node within the current zone that also
// borders another zone. We use a CALL subquery to find all
// potential end nodes.
CALL {
MATCH ()-[:$(zone)]-(end)-[o:!$(zone)]-()
// We add a condition for which exits are valid:
// EITHER this is the last zone (i = numZones), so any border
// node is a valid end node, OR the end node must lead to a zone
// we haven't visited yet.
WHERE i = numZones OR NOT type(o) IN pathAcc.visited
RETURN DISTINCT end
}
// ------ FIND THE PATH ------
// We use ALL SHORTEST to find all paths from our start s to a
// valid end that traverses all relationships in rels.
// The REPEATABLE ELEMENTS feature allows us to do the backtracking
// necessary. The limit 13 is a performance hint.
MATCH REPEATABLE ELEMENTS ALL SHORTEST (
p = (s)-[r:$(zone)]-{,13}(end)
WHERE
s = pathAcc.start AND
all(rel IN rels WHERE rel IN relationships(p))
)
// ------ SELECT THE BEST PATH ------
// ALL SHORTEST finds paths with the minimum number of hops.
// There might be multiple such paths. To pick the "best" one, we
// calculate a more realistic distance for each path: the Manhattan
// Distance, using the node coordinates.
LET distance = reduce(
disAcc = {distance: 0, prev: s},
n IN nodes(p) |
{
distance: disAcc.distance
+ abs(disAcc.prev.x - n.x)
+ abs(disAcc.prev.y - n.y),
prev: n
}
).distance
// We order the paths by their Manhattan distance and pick the
// shortest one (or the first, if there is more than one of the
// same length).
ORDER BY distance
LIMIT 1
// ------ UPDATE THE ACCUMULATOR FOR THE NEXT ITERATION ------
// Now that we have the optimal path p for the current zone, we
// return a new map. This map will become the value of pathAcc for
// the next loop iteration.
RETURN {
// The start node for the next zone is the end node of this zone.
start: end,
// Append the sequence of junction numbers from path p to our
// master sequence.
seq: pathAcc.seq + [[node IN nodes(p) | node.junction]],
// Add the zone we just cleared to the list of visited zones.
visited: pathAcc.visited + [zone]
}
}[0] // The [0] selects the single map returned by the COLLECT subquery.
// Finally, after the reduce loop has finished, the accumulator pathAcc will
// contain the complete solution. We only care about the sequence of moves.
).seq AS pathsThe result is a list of four lists, the sequence of junctions within each zone, with the zones in order:
+------------------------------------------------------------+
| paths |
+------------------------------------------------------------+
| [[23, 24, 20, 28, 26, 28, 30, 29, 30, 25, 24, 25, 26, 20], |
| [20, 14, 9, 10, 14, 10, 2, 9, 8, 13, 8, 7, 2, 7] |
| [7, 6, 1, 3, 4, 1, 6, 5, 12, 5, 4, 11, 3, 11], |
| [11, 17, 27, 29, 22, 21, 27, 21, 17, 23, 22, 23]] |
+------------------------------------------------------------+The junction numbers at the starts and ends of each list line up so the sub-paths form one overall path for Pac-Man to take. For example, the first path ends at junction 20, so the second path begins at 20, the second path ends at 7, so the third starts at 7, etc.
Visualizing the four paths on top of the board makes the solution clearer:
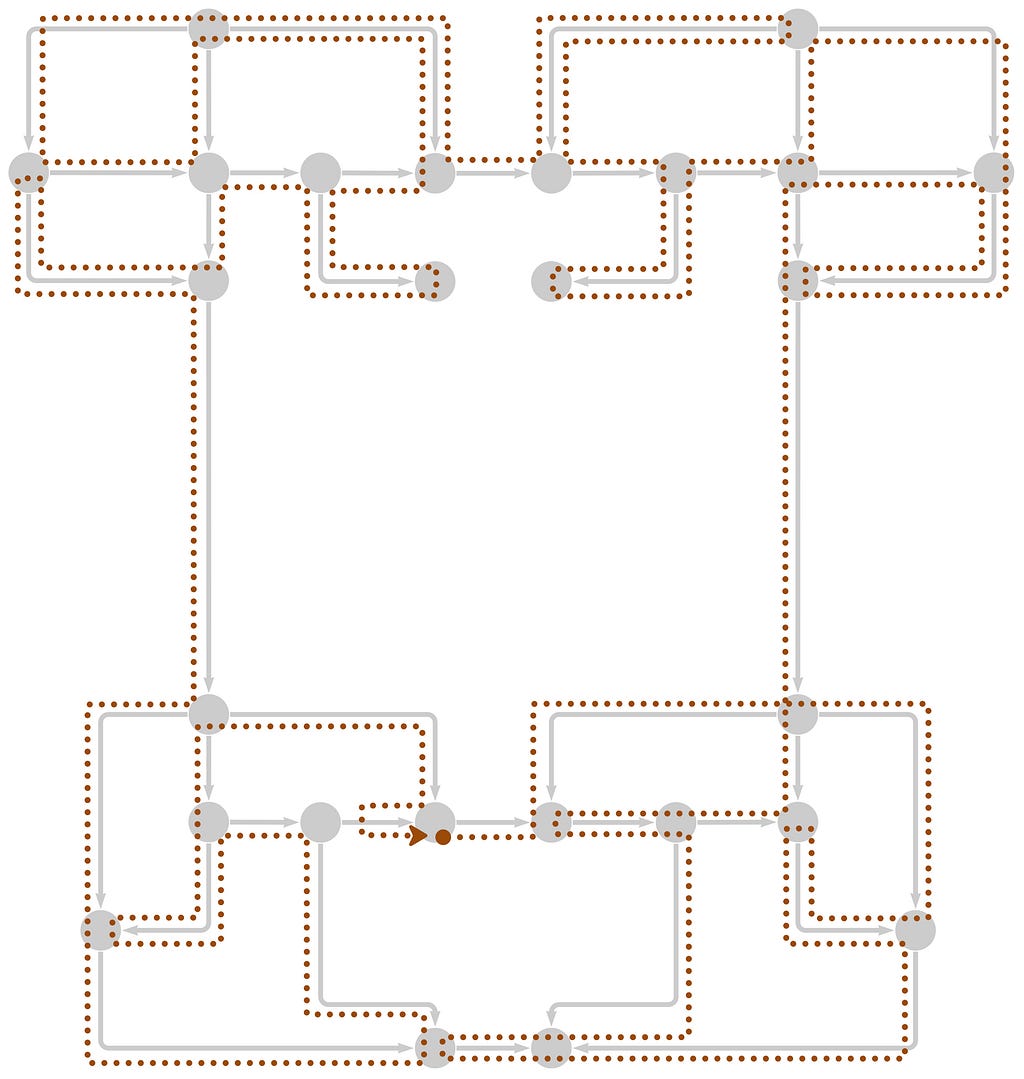
We used LIMIT 1 in the query to pick just one of the optimal length paths in each zone, so there are other possible solutions. But given that the conditions for a Eulerian path or circuit allow either 2 or 0 nodes with odd degree, respectively, it’s safe to say that most graphs you might encounter will require doubling back to cover every relationship.
Summary
Cypher 25 introduced a new match mode, REPEATABLE ELEMENTS, which is essential for finding paths with backtracking or cycle repetition. These paths crop up in a number of places: optimal pathfinding with constraints (e.g., finding the shortest detour for a gas station), covering path problems (e.g., optimizing a doctor’s rounds), and peer-to-peer reachability in a hierarchical structure (e.g., finding relatives with a grandparent in common).
The downside of allowing doubling back with REPEATABLE ELEMENTS is that the number of possible paths increases considerably with the size of the graph. So whenever using REPEATABLE ELEMENTS with variable-length paths, care needs to be taken to constrain the solutions (e.g., ask for just the shortest path, put a limit on path lengths, divide the problem into multiple smaller problems). This is true of variable-length paths in general, of course, only more so with REPEATABLE ELEMENTS.
Resources
- Cypher documentation on match modes
- I Would Walk 500 Miles
- Cypher Versioning
- Neo4j AuraDB
- Release Notes: Neo4j Aura Database – June 2025
- Release Notes: Neo4j 2025.06
Query, Chomp, Repeat was originally published in Neo4j Developer Blog on Medium, where people are continuing the conversation by highlighting and responding to this story.