Going Underground: Graphing and Pathfinding London Tube Lines

Senior Pre-Sales Consultant, Neo4j
6 min read
Living in London, hardly a day goes by when I don’t use the public transportation system. I ride the Tube every day I go to work in the office, and over the past nine years I’ve come to know large portions of the iconic Tube map like the back of my hand.
The thing about the Tube map is (naturally) it looks like a graph. They even use circles to make Stations look like nodes, and the Lines are like relationships, just the way I’d model it in Neo4j!
“Pathfinding” is a very common use case for graph databases, and I’ve always wondered if any of the popular journey planning tools use a graph to help Tube riders find their way (Top Tip: As is true for most major cities, don’t visit London without Citymapper installed on your phone).
I did a bit of digging and found some data available that I could use to model the Tube network in Neo4j and show how pathfinding can be applied to some real-world examples. The data is a few years old, and doesn’t include all of the London Overground stations, but it’s good enough to demonstrate what a great fit a graph database is for this use case. The data includes longitude and latitude for each station (which will be useful later) as well as the time it takes to ride each line between any two stations.
The “Meta-Graph” I created for this example is pretty simple. Stations are connected to other Stations by relationships labelled by line (i.e. NORTHERN, CENTRAL, etc.). Stations can also be ‘ON’ a Line, as well as ‘IN_ZONE’ (since the cost of a ride on the Tube is determined by how many zones you travel in).
call db.schema()
In the loaded graph, a Station can be ‘ON’ multiple lines, and some Stations are linked to more than one Zone (like Archway, which is in both Zones 2 and 3). The direction of the individual Line relationships isn’t important, as you can generally travel in both directions between stations.
When I loaded the data into our graph I ended up with 324 nodes and 1150 relationships – not the biggest graph in the world, but still a lot of stations and connections for one Tube network!
Visualizing all the stations and connections in one graph is a bit difficult (particularly when they’re not laid out like the traditional Tube map), as you can see:
MATCH path = (:Station)-[]->(:Station) RETURN *
An easier view is to look at one line, end to end. The line I ride the most is the Northern Line, which in our graph looks like this:
MATCH path = (a:Station)-[:NORTHERN]-(b:Station) RETURN path
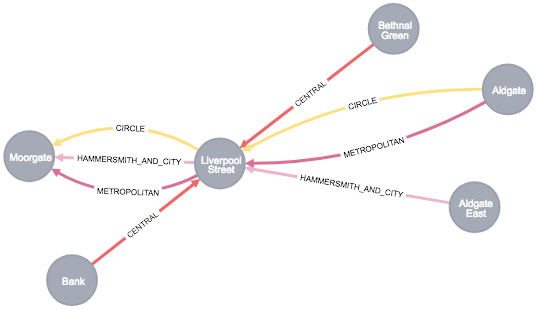
We could take an even more detailed view and look at one Station and its direct connections. I chose the busy Liverpool Street Station, which is on several lines:
MATCH path = (:Station {name: 'Liverpool Street'})-[]-(:Station) RETURN path
You see that from Liverpool Street you can travel directly to Moorgate, Bank, Bethnal Green, Aldgate or Aldgate East using the Tube.
Now that our data is in place, and we’ve seen how it looks, it’s time to get down to some pathfinding!
First, since we know the latitude and longitude for each Tube station, we can find the one closest to the Neo4j London offices (which, thanks to Google Maps, I know is located at 51.505483, -0.104920).
MATCH (near:Station)
WITH near, point(near) AS start, point({latitude: 51.505483, longitude: -0.104920 }) AS neo4j
WITH near, distance(start, neo4j) AS distance
RETURN near, distance ORDER BY distance ASC LIMIT 1
The nearest station in our data set is Southwark (pronounced SUTH-uck, for those who don’t speak British English), which is a block away from the Neo4j offices on Blackfriar’s Road. This is called a “Geospatial query,” because we’re using the latitude and longitude of the Tube stations in our data set (their geospatial data) to make our query rather than following relationships or matching the values of properties on the nodes.
Building on that query, I can then find all the shortest paths (measured by the number of “hops” or relationships traversed) from Southwark Station to Liverpool Street Station.
MATCH (near:Station)
WITH near, point(near) AS start, point({latitude: 51.505483, longitude: -0.104920 }) AS neo4j
WITH near, distance(start, neo4j) AS distance ORDER BY distance ASC LIMIT 1
MATCH path = allShortestPaths( (near)-[:NORTHERN|CIRCLE|CENTRAL|EAST_LONDON|DISTRICT|METROPOLITAN|HAMMERSMITH_AND_CITY|EAST_LONDON|VICTORIA|WATERLOO_AND_CITY|BAKERLOO|DLR|PICADILLY|JUBILEE*]-(:Station {name: 'Liverpool Street'}) )
RETURN path
We can see that the shortest routes between Southwark and East Finchley (measured by the number of hops in the graph) involves 4 stations and uses 3 different Tube lines. We have two options – we can travel West from Southwark to Waterloo and on to Bank, or we can travel East from Southwark to London Bridge and on to Bank.
“Number of hops” isn’t the only measure of “length” we have for our journey, though. Since our data set includes a measure of time for how long it takes to travel each line between stations, we can use this as a weight for computing the quickest path.
For this, we’ll use one of the Neo4j graph algorithms designed to find weighted shortest paths – using our nearest station as the start, Liverpool Street Station as the end and the “time” property on each relationship as our weight.
MATCH (near:Station), (end:Station {name: 'Liverpool Street'})
WITH near, end,point(near) AS start, point({latitude: 51.505483, longitude: -0.104920 }) AS neo4j
WITH near, end, distance(start, neo4j) AS distance ORDER BY distance ASC LIMIT 1
CALL algo.shortestPath.stream(near, end, 'time', {nodeQuery: 'Station'}) YIELD nodeId, cost
RETURN algo.getNodeById(nodeId)
Here we can see that the quickest route from Southwark to Liverpool Street is via London Bridge and Bank – which makes sense, as it would be slower to ride West to Waterloo only to head farther east again to Bank Station. If you want to ride the Tube like a pro, it’s all about minimizing travel time! (And standing on the right when riding the escalators, but that’s another blog post.)
Hopefully you’ve seen how the connected structure of a graph makes finding paths through real-world networks – like the London Underground Network – not only possible but also quick and intuitive. This was a pretty simple example – there are so many ways we could extend our data and queries to make it a fully functional journey planning system.
Some additional ideas might include:
- Mapping bus and rail connections, so that we can plan routes across London using several types of public transportation.
- Limiting the number of line transfers required for a journey. Every time you need to transfer between lines you add time, and potential risk (if the trains are delayed or suspended), to your journey!
- Returning the cheapest journey by limiting how many zones a journey passes through.
- Providing more detail about each station, like whether they offer step-free access and how far the distance between platforms for particular line transfers is. This way you could plan routes for riders with special needs, like wheelchair users.
Remember, “The world is your oyster.” Mind the Gap, and happy travels!
[Did you know that the London Underground had its origins in the Metropolitan Railway, the world’s first underground passenger railway, opened in 1863? It kinda shows – the current Tube network groans under the weight of the 1.4 billion passengers who use it every year (based on the 2017/18 figures). Up to 5 million people ride the tube every day! It’s no wonder I always have such a hard time getting a seat.
Still, the Underground is a real engineering marvel and Londoners (and those who visit and work in London) couldn’t really live without it. The network has hundreds of stations and hundreds of miles of tracks all across the city and the extended metropolitan London area, though South London doesn’t have as much coverage as we do north of the Thames. Using public transport is an economical, easy, relatively fast (compared to driving) and green way to get around London. If you’re visiting, you have to ride the Tube… it’s the only way you can really feel you know London!]