Graph Algorithms in Neo4j: Label Propagation
4 min read

Graph algorithms provide the means to understand, model and predict complicated
dynamics such as the flow of resources or information, the pathways through which
contagions or network failures spread, and the influences on and resiliency of groups.
This blog series is designed to help you better utilize graph analytics and graph algorithms so you can effectively innovate and develop intelligent solutions faster using a graph database like Neo4j.
Last week we continued our look at Community Detection algorithms, with our focus on the Weakly Connected Components algorithm.
This week we continue our exploration of Community Detection algorithms, with a look at the Label Propagation algorithm, which spreads labels based on neighborhood majorities as a means of inferring clusters. This extremely fast graph
partitioning requires little prior information and is widely used in large-scale networks for community detection.
About Label Propagation
The Label Propagation algorithm (LPA) is a fast algorithm for finding communities in a graph. It detects these communities using network structure alone as its guide and doesn’t require a predefined objective function or prior information about the communities.
One interesting feature of LPA is that you have the option of assigning preliminary labels to narrow down the range of generated solutions. This means you can use it as a semi-supervised way of finding communities where you handpick some initial communities.
LPA is a relatively new algorithm and was only proposed by Raghavan et al. in 2007, in Near linear time algorithm to detect community structures in large-scale networks.” It works by propagating labels throughout the network and forming communities based on this process of label propagation.
The intuition behind the algorithm is that a single label can quickly become dominant in a densely connected group of nodes, but it will have trouble crossing a sparsely connected region. Labels will get trapped inside a densely connected group of nodes, and those nodes that end up with the same label when the algorithm finishes are considered part of the same community.
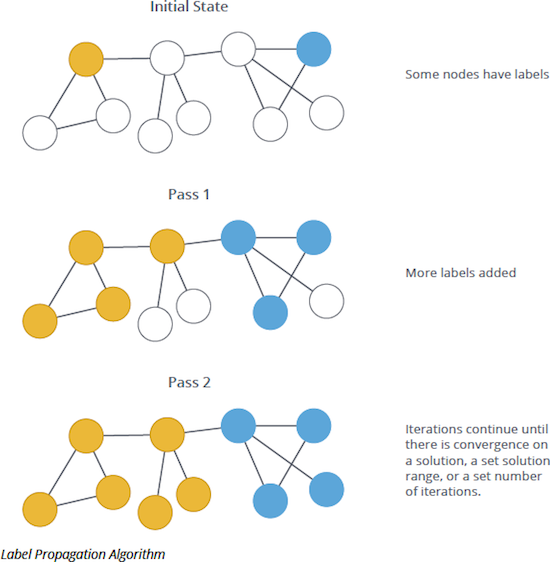
NOTE: The algorithm works as follows:
- Every node is initialized with a unique label (an identifier).
- These labels propagate through the network.
- At every iteration of propagation, each node updates its label to the one that the maximum number of its neighbors belongs to. Ties are broken uniformly and randomly.
- LPA reaches convergence when each node has the majority label of its neighbors. As labels propagate, densely connected groups of nodes quickly reach a consensus on a unique label. At the end of the propagation, only a few labels will remain – most will have disappeared. Nodes that have the same label at convergence are said to belong to the same community.
When Should I Use Label Propagation?
- Label Propagation has been used to assign polarity of tweets, as a part of semantic analysis that uses seed labels from a classifier trained to detect positive and negative emoticons in combination with the Twitter follower graph. For more information, see Twitter polarity classification with label propagation over lexical links and the follower graph.”
- Label Propagation has been used to estimate potentially dangerous combinations of drugs to co-prescribe to a patient, based on the chemical similarity and side effect profiles. The study is found in Label Propagation Prediction of Drug-Drug Interactions Based on Clinical Side Effects.”
- Label Propagation has been used to infer features of utterances in a dialogue for a machine learning model to track user intention with the help of a Wikidata knowledge graph of concepts and their relations. For more information, see Feature Inference Based on Label Propagation on Wikidata Graph for DST.”
TIP: In contrast with other algorithms, Label Propagation results in different community structures when run multiple times on the same graph. The range of solutions is narrowed if some nodes are given preliminary labels, while others are unlabeled. Unlabeled nodes are more likely to adopt the preliminary labels.
Label Propagation Example
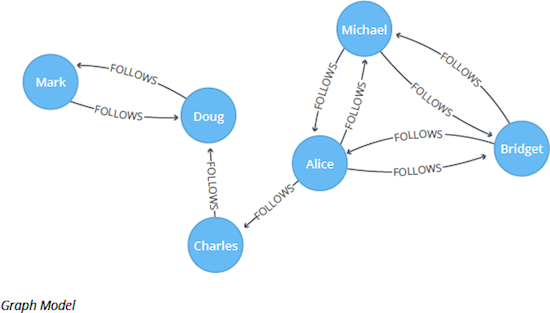
Let’s see the Label Propagation algorithm in action. The following Cypher statement creates a Twitter-esque graph containing users and FOLLOWS relationships between them.
MERGE (nAlice:User {id:"Alice"})
MERGE (nBridget:User {id:"Bridget"})
MERGE (nCharles:User {id:"Charles"})
MERGE (nDoug:User {id:"Doug"})
MERGE (nMark:User {id:"Mark"})
MERGE (nMichael:User {id:"Michael"})
MERGE (nAlice)-[:FOLLOWS]->(nBridget)
MERGE (nAlice)-[:FOLLOWS]->(nCharles)
MERGE (nMark)-[:FOLLOWS]->(nDoug)
MERGE (nBridget)-[:FOLLOWS]->(nMichael)
MERGE (nDoug)-[:FOLLOWS]->(nMark)
MERGE (nMichael)-[:FOLLOWS]->(nAlice)
MERGE (nAlice)-[:FOLLOWS]->(nMichael)
MERGE (nBridget)-[:FOLLOWS]->(nAlice)
MERGE (nMichael)-[:FOLLOWS]->(nBridget)
MERGE (nCharles)-[:FOLLOWS]->(nDoug);
Now we run LPA to find communities among the users. Execute the following query:
CALL algo.labelPropagation.stream("User", "FOLLOWS",
{direction: "OUTGOING", iterations: 10})
Our algorithm found two communities with three members each.
It appears that Michael, Bridget and Alice belong together, as do Doug and Mark. Only Charles doesn’t strongly fit into either side, but ends up with Doug and Mark.
Conclusion
As we’ve seen, the Label Propagation algorithm has diverse applications from
understanding consensus formation in social communities to identifying sets of proteins that are involved together in a process (functional modules) for biochemical networks.
Next week we’ll continue our focus on Community Detection algorithms, with a look at the Louvain Modularity algorithm.
Learn about the power of graph algorithms in the O’Reilly book,
Graph Algorithms: Practical Examples in Apache Spark and Neo4j by the authors of this article. Click below to get your free ebook copy.