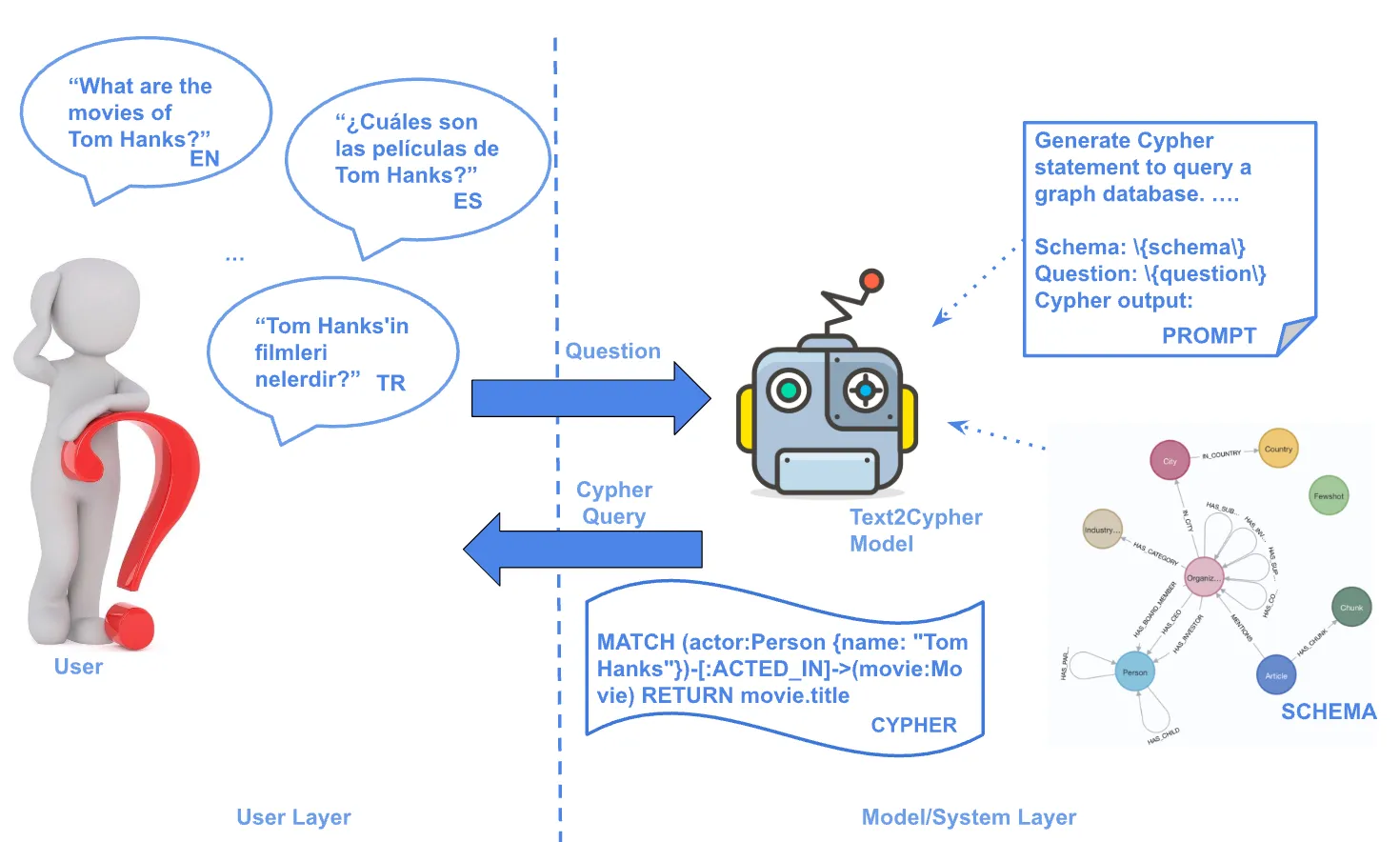
Graph Algorithms in Neo4j: PageRank
5 min read

Graph algorithms provide the means to understand, model and predict complicated dynamics such as the flow of resources or information, the pathways through which contagions or network failures spread, and the influences on and resiliency of groups.
This blog series is designed to help you better utilize graph analytics and graph algorithms so you can effectively innovate and develop intelligent solutions faster using a graph database.
Last week we finished our look at pathfinding and graph search algorithms, with a focus on Minimum Weight Spanning Tree.
This week we begin our exploration of Centrality algorithms, with a look at PageRank, which estimates a current node’s importance from its linked neighbors and then again from their neighbors, using examples from Neo4j.
One interesting bit of trivia about PageRank: It is named after Google cofounder Larry Page, and is used to rank websites in Google’s search results.
About PageRank
PageRank is an algorithm that measures the transitive, or directional, influence of nodes. All other centrality algorithms we discuss measure the direct influence of a node, whereas PageRank considers the influence of your neighbors and their neighbors.
For example, having a few influential friends could raise your PageRank more than just having a lot of low-influence friends.
PageRank is computed by either iteratively distributing one node’s rank (originally based on degree) over its neighbors or by randomly traversing the graph and counting the frequency of hitting each node during these walks.
PageRank counts the number and quality of links to a page, which determines an estimation of how important the page is. The underlying assumption is that pages of importance are more likely to receive a higher volume of links from other influential pages.
NOTE: PageRank is defined in the original Google paper as follows:
PR(A) = (1-d) + d (PR(T1)/C(T1) + ... + PR(Tn)/C(Tn))
where,
- we assume that a page
Ahas pagesT1toTnwhich point to it (i.e., are citations).dis a damping factor which is set between 0 and 1. It is usually set to 0.85.C(A)is defined as the number of links going out of pageA.
When Should I Use PageRank?
PageRank can be applied across a wide range of domains. The following are some notable use cases:
-
- Personalized PageRank is used by Twitter to present users with recommendations of other accounts that they may wish to follow. The algorithm is run over a graph that contains shared interests and common connections. Their approach is described in more detail in “WTF: The Who to Follow Service at Twitter.”
- PageRank has been used to rank public spaces or streets, predicting traffic flow and human movement in these areas. The algorithm is run over a graph that contains intersections connected by roads, where the PageRank score reflects the tendency of people to park, or end their journey, on each street. This is described in more detail in “Self-Organized Natural Roads for Predicting Traffic Flow: A Sensitivity Study.”
- PageRank is also used as part of an anomaly or fraud detection system in the healthcare and insurance industries. It helps find doctors or providers that are behaving in an unusual manner and then feeds the score into a machine learning algorithm.
There are many more use cases for PageRank described in David Gleich’s paper, “PageRank Beyond the Web.”
TIP: There are some things to be aware of when using the PageRank algorithm:
- If there are no links from within a group of pages to outside of the group, then the group is considered a spider trap.
- Rank sink occurs when a network of pages forms an infinite cycle.
- Dead-ends occur when pages have no out-links. If a page contains a link to a dead end page, the link is known as a dangling link.
If you see unexpected results from running the algorithm, it is worth doing some exploratory analysis of the graph to see if any of these problems are the cause. You can read The Google PageRank Algorithm and How It Works to learn more.
PageRank Example
Let’s calculate PageRank on a small dataset.
The following Cypher statement creates a sample graph of web pages and links between them.
MERGE (home:Page {name:"Home"})
MERGE (about:Page {name:"About"})
MERGE (product:Page {name:"Product"})
MERGE (links:Page {name:"Links"})
MERGE (a:Page {name:"Site A"})
MERGE (b:Page {name:"Site B"})
MERGE (c:Page {name:"Site C"})
MERGE (d:Page {name:"Site D"})
MERGE (home)-[:LINKS]->(about)
MERGE (about)-[:LINKS]->(home)
MERGE (product)-[:LINKS]->(home)
MERGE (home)-[:LINKS]->(product)
MERGE (links)-[:LINKS]->(home)
MERGE (home)-[:LINKS]->(links)
MERGE (links)-[:LINKS]->(a)
MERGE (a)-[:LINKS]->(home)
MERGE (links)-[:LINKS]->(b)
MERGE (b)-[:LINKS]->(home)
MERGE (links)-[:LINKS]->(c)
MERGE (c)-[:LINKS]->(home)
MERGE (links)-[:LINKS]->(d)
MERGE (d)-[:LINKS]->(home)
Now we run the PageRank algorithm to calculate the most influential pages. Execute the following query.
CALL algo.pageRank.stream("Page", "LINKS",
{iterations:20})
YIELD nodeId, score
MATCH (node) WHERE id(node) = nodeId
RETURN node.name AS page,score
ORDER BY score DESC
As we might expect, the Home page has the highest PageRank because it has incoming links from all other pages. Also, it’s not only the number of incoming links that is important, but also the importance of the pages behind those links.
Conclusion
As we’ve seen, PageRank is used to estimate importance and influence, to suggest Twitter accounts to follow and for general sentiment analysis.
Next week, we’ll have a look at another Centrality algorithm – Degree Centrality, – which measures the number of relationships a node has. It’s broken into indegree (flowing in) and outdegree (flowing out) where relationships are directed.
Learn about the power of graph algorithms in the O’Reilly book,
Graph Algorithms: Practical Examples in Apache Spark and Neo4j by the authors of this article. Click below to get your free ebook copy.Get the O’Reilly Ebook