Graph Algorithms in Neo4j: Weakly Connected Components
3 min read

Graph algorithms provide the means to understand, model and predict complicated
dynamics such as the flow of resources or information, the pathways through which
contagions or network failures spread, and the influences on and resiliency of groups.
This blog series is designed to help you better utilize graph analytics and graph algorithms so you can effectively innovate and develop intelligent solutions faster using a graph database like Neo4j.
Last week we started our look at Community Detection algorithms, with our look at the Strongly Connected Components algorithm.
This week we continue our exploration of these algorithms, with a look at the Weakly Connected Components algorithm, which finds groups of nodes where each node is reachable from any other node in the same group, regardless of the direction of relationships.
About Weakly Connected Components (Union Find)
The Weakly Connected Components, or Union Find, algorithm finds sets of connected nodes in an undirected graph where each node is reachable from any other node in the same set.
It differs from the Strongly Connected Components algorithm (SCC) because it only needs a path to exist between pairs of nodes in one direction, whereas SCC needs a path to exist in both directions. As with SCC, Union Find is often used early in an analysis to understand a graph’s structure.
Bernard A. Galler and Michael J. Fischer first described this algorithm in 1964. The components in a graph are computed using either the breadth-first search or depth-first search algorithms.
When Should I Use Union Find?
- Testing whether a graph is connected is an essential pre-processing step for every graph algorithm. Such tests are performed so quickly and easily that you should always verify that your input graph is connected, even when you know it has to be. Subtle, difficult-to-detect bugs often result when your algorithm is run only on one component of a disconnected graph.
- Union Find is also used to keep track of clusters of database records, as part of the de-duplication process – an important task in master data management applications. Read more in An Efficient Domain-Independent Algorithm for Detecting Approximately Duplicate Database Records.”
- Weakly Connected Components (WCC) is used to analyze citation networks as well. One study uses WCC to work out how well-connected the network is, and then to see whether the connectivity remains if “hub” or “authority” nodes are moved from the graph. Read more in “Characterizing and Mining Citation Graph of Computer Science Literature.”
Union Find Example
Let’s see the Union Find algorithm in action. The following Cypher statement creates a graph of people and their friends.
MERGE (nAlice:User {id:"Alice"})
MERGE (nBridget:User {id:"Bridget"})
MERGE (nCharles:User {id:"Charles"})
MERGE (nDoug:User {id:"Doug"})
MERGE (nMark:User {id:"Mark"})
MERGE (nMichael:User {id:"Michael"})
MERGE (nAlice)-[:FRIEND]->(nBridget)
MERGE (nAlice)-[:FRIEND]->(nCharles)
MERGE (nMark)-[:FRIEND]->(nDoug)
MERGE (nMark)-[:FRIEND]->(nMichael);
Now we run Union Find to find connected components. Execute the following query.
CALL algo.unionFind.stream("User", "FRIEND", {})
YIELD nodeId,setId<
MATCH (u:User) WHERE id(u) = nodeId
RETURN u.id AS user, setId
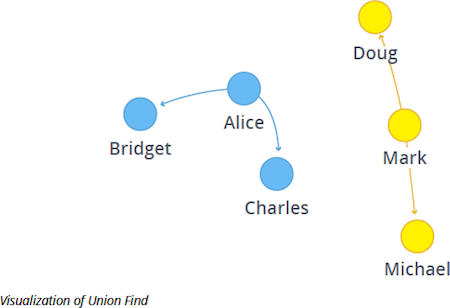
We have two distinct groups of users that have no link between them.
The first group contains Alice, Charles and Bridget, while the second group contains Michael, Doug and Mark.
Conclusion
As we’ve seen, the Weakly Connected Components algorithm is often used to enable running other algorithms independently on an identified cluster. As a preprocessing step for directed graphs, it helps quickly identify disconnected groups.
Next week we’ll continue our focus on Community Detection algorithms, with a look at Label Propagation.
Learn about the power of graph algorithms in the O’Reilly book,
Graph Algorithms: Practical Examples in Apache Spark and Neo4j by the authors of this article. Click below to get your free ebook copy.