Social Networks in the Database: Using a Graph Database

Neo4j Documentation Manager
10 min read
Recently Lorenzo Alberton gave a talk on Trees In The Database where he showed the most-used approaches to storing trees in a relational database. Now he has moved on to an even more interesting topic with his article Graphs in the database: SQL meets social networks. Right from the beginning of his excellent article Alberton puts this technical challenge in a proper context:
Graphs are ubiquitous. Social or P2P networks, thesauri, route-planning systems, recommendation systems, collaborative filtering, even the World Wide Web itself is ultimately a graph! Given their importance, it’s surely worth spending some time in studying some algorithms and models to represent and work with them effectively.
After a brief explanation of what a graph data structure is, the article goes on to show how graphs can be represented in a table-based database. The rest of the article shows in detail how an adjacency list model can be used to represent a graph in a relational database. Different examples are used to illustrate what can be done in this way.
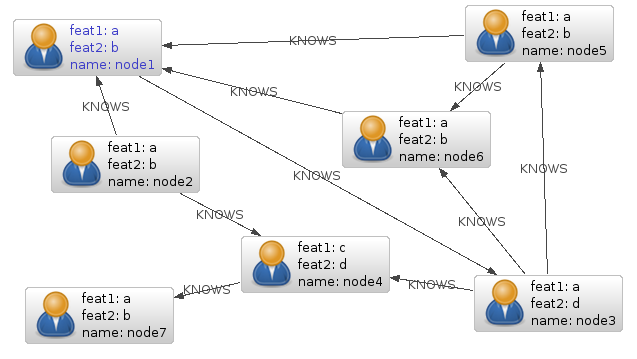
This post is going to show how the same things can be done when using a native graph database, namely Neo4j. To begin with, it’s good to have a grip on how your data actually looks, and when it comes to graphs I prefer a graphical representation, so here goes:
As you can see, it’s a fairly small social network, so it should be easy to comprehend what’s going on in the examples. Anyhow, please read the original article for the full context of the examples; this article will mainly deal with how to solve the same problems in a true graph database. For the sample code, Java will be used. If you’re no fan of Java, go check out the current language drivers for Neo4j.
Representing a Graph
This part is very different when dealing with a graph database: there’s no need to think much about the representation at all when using a graph database. Nodes and relationships (also called edges) are native to a graph database and this includes making sure that the graph is consistent (for example ensuring that every relationship has a start node and an end node). As a developer you can focus more on what to model and less on how to represent it.
Traversing the Graph
Our first task is to find the nodes that are directly connected to a node in the case of directed relationships. We assume the node variable as input and then the code is as easy as follows:
for ( Relationship rel : node.getRelationships( RelationshipTypes.KNOWS, Direction.OUTGOING ) )
{
Node otherNode = rel.getEndNode();
// Here goes your code to make use of otherNode.
// You can aggregate it or whatever you want to do.
}
What we are doing here is to fetch all the outgoing relationships and then get the node at the other end of the relationship. In Neo4j, all relationships between nodes are typed, and as seen from both the image above and the code, a KNOWS relationship type was used in this case. The relationship types are explained on the RelationshipType page of the Neo4j API reference.
The following image shows node1 and all the nodes that are directly connected to it. When following all outgoing relationships, the result will be a single node, namley node3.
Next, it’s time to do the same thing again but using undirected relationships. Both Neo4j and the model in Alberton’s article store the relationships as directed but then you can retrieve them in a different way to ignore their direction. Here’s how to do this using Neo4j:
for ( Relationship rel : node.getRelationships( RelationshipTypes.KNOWS, Direction.BOTH ) )
{
Node otherNode = rel.getOtherNode( node );
// Make use of otherNode here ...
}
Did you spot the difference? Where the previous code had Direction.OUTGOING we know have Direction.BOTH. For those of you who are curious now: yes, there’s Direction.INCOMING as well.
When viewed with a perspective that ignores directions, the whole graph looks like this:
When running the new code with Direction.BOTH, all the directly connected nodes will be retrieved irregardless of direction:
Difference between graph-based/table-based: First, obviously the SQL solution is declarative, while the Neo4j solution is procedural. As we’ll see later on there is a declarative API to traverse the node space (graph) in Neo4j as well. Second, changing from directed to undirected relationships almost didn’t change the code necessary at all with the graph database approach, while the relational one requires some changes.
Transitive Closure
Transitive closure, in the sense Alberton uses it, is irrelevant in a graph database context as you have access to the full graph from the beginning. The need for defining a transitive closure over the graph in relational databases is caused by its lack of native support for graph data structures.
What is still of course relevant in the graph database setting is how to find all nodes that are reachable from one node, using directed relationships. So let’s see how to do that. As previously we assume the node variable as input to this piece of code:
Traverser traverser = node.traverse(
Order.BREADTH_FIRST,
StopEvaluator.END_OF_GRAPH,
ReturnableEvaluator.ALL_BUT_START_NODE,
RelationshipTypes.KNOWS,
Direction.OUTGOING );
for ( Node foundNode : traverser )
{
final int depth = traverser.currentPosition().depth();
// Use foundNode and depth to whatever you want.
}
So what’s happening in this code? We start out by setting up a traverser. The traverser will use a breadth first algorithm, so that we can intercept the depth/distance to each of the returned node correctly. The traverser will not stop until the end of the graph and will return all nodes but the start node. It will follow relationships of the KNOWS type in the outgoing direction. Finally the loop fetches the result from the traverser.
If we for some reason want to do this for all nodes in the graph, we simply feed the code above with all existing nodes. This time we assume having all nodes in our network in the allNodes variable. It’s easy to get them as the Neo Service API provides a getAllNodes() method. What we need to do is just a regular loop:
for ( Node node : allNodes )
{
// perform the traversal for each node here
}
How then to do the same thing but using undirected relationships? I am rest assured that readers will have no problems solving this so I leave it as a homework exercise!
Difference between graph-based/table-based: This time it’s less obvious what the SQL actually does; you need a bit of SQL fu to parse that code! The corresponding Neo4j code this time uses a declarative approach, which depicts the wanted result.
LinkedIn: Degrees of Separation
Now it’s definitely time to get closer to what a graph database could do for you in an application. In this case, we want to know the possible paths from one person in a social network to an other. With those paths at hand we can do things similar to the “How you’re connected to N.N.” feature of LinkedIn.
For a deeper analysis, it could be of interest to know all possible paths between two nodes within a limited distance (and not only go for the shortest path), so we will see how that would work. This task could be performed with the low-level API of Neo4j, but in this case we will use the graph-algo package instead.
Of course a graph database should come with basic graph algorithms included as well! This time we will assume that we (quite obviously) know the start and end nodes and how long the paths are that we’re looking for (maxPathLength). Let’s get to the code:
AllSimplePaths simplePaths = new AllSimplePaths(
startNode,
endNode,
maxPathLenght,
Direction.BOTH,
RelationshipTypes.KNOWS );
List<List<Node>> pathsAsNodes = simplePaths.getPathsAsNodes();
// Use pathsAsNodes in your application.
Do you want to sort the paths by distance (a.k.a. lenght of the paths)? Then add this code:
Collections.sort( pathsAsNodes, new Comparator<List<Node>>()
{
public int compare( final List<Node> left, final List<Node> right )
{
return left.size() - right.size();
}
} );
When looking for paths from node1 to node6 using undirected relationships, all nodes but node7 will be part of at least one path:
If we for some reason use directed relationships, the result will be found among the nodes that are colored yellow in this graph:
Difference between graph-based/table-based: In this case, you could argue that it’s not a fair comparison, since a relational database can’t ship with built-in functions for such specific things as finding paths in a graph. There’s some validity to that. But that’s also my point: Graphs are, as Alberton and Google say, ubiquitous these days and no longer a niche technology. In an increasingly connected world, a graph database many times brings a lot more functionality and performance to the table – pun intended! – than a relational system designed for the payroll systems of the 70s.
Facebook: You Might Also Know
Our last example will require some more complexity to solve. But on the other hand I regard it as the most fun and rewarding piece.
The challenge this time is to traverse into friends of friends (or even deeper) and find people with something in common. Based on this we can distill someone the user might know, or could be interested in knowing. The persons in our social network all have different values for two features, feat1 and feat2. The idea of the solution presented here is to keep track of the features that are common in each branch of the traversal and to stop when there is nothing in common any more or the maximum distance has been reached.
To do this we use recursion (which was never a problem in graph databases, unlike in relational database systems). Before we start to recurse, we have to set some things up:
class YouMightKnow
{
List<List<Node>> result = new ArrayList<List<Node>>();
int maxDistance;
Set<Node> buddies = new HashSet<Node>();
public YouMightKnow( Node node, String[] features, int maxDistance )
{
this.maxDistance = maxDistance;
for ( Relationship rel : node.getRelationships( RelationshipTypes.KNOWS ) )
{
buddies.add( rel.getOtherNode( node ) );
}
findFriends( node, Arrays.asList( new Node[] { node } ), Arrays.asList( features ), 1 );
}
The features parameter contains the names of the features we want to check. As all features of course matches at the starting point, we can send them in as the matches list. To make sure we don’t suggest people who are already buddies we keep track of those in a set.
That’s all we need to prepare, so off we go to the recursion! It’s initially fed with the root node and path to start from, together with the list of the matching features and finally the current distance. Here’s how things continue from there:
void findFriends( Node rootNode, List<Node> path, List<String> matches, int depth )
{
for ( Relationship rel : rootNode.getRelationships( RelationshipTypes.KNOWS ) )
{
Node node = rel.getOtherNode( rootNode );
if ( (depth > 1 && buddies.contains( node )) || path.contains( node ) )
{
continue;
}
List<String> newMatches = new ArrayList<String>();
for ( String match : matches )
{
if ( node.getProperty( match ).equals( rootNode.getProperty( match ) ) )
{
newMatches.add( match );
}
}
if ( newMatches.size() > 0 )
{
List<Node> newPath = new ArrayList<Node>( path );
newPath.add( node );
if ( depth > 1 )
{
result.add( newPath );
}
if ( depth != maxDistance )
{
findFriends( node, newPath, newMatches, depth + 1 );
}
}
}
}
}
Now there’s a few things we need to think about to get this code right. It’s not hard if you keep the network structure in your mind. To begin with there are some nodes we have to avoid. As soon as we have passed by (depth > 1) the buddies, we don’t want to meet them again. We also want to avoid nodes which are already contained in the path we are investigating, thus avoiding cycles in the graph.
When we know we are looking at the right nodes, it’s time to compare their features. We only look at the features that are matching everyone in the path behind us, so the newMatches list will get shorter than the matches list if one or more features don’t match any more. If there are no newMatches we’re finished with this branch. Otherwise we construct a newPath. Then we have to make sure not to add buddies to the result and to stop recursing when the maxDistance has been reached.
Finally, this is how to use the class:
String[] features = new String[] { "feat1", "feat2" };
YouMightKnow mightKnow = new YouMightKnow( node5, features, 2 );
// get result from mightKnow.result
The graphical view of this problem looks like this, when searching for “might-know” nodes of node5:
If you would like to do something more advanced it would be a small step to add in you own feature matching operations instead of the simple equals() method used in this example.
Difference between graph-based/table-based: If you compare the code, you’ll note that the graph database code is more intuitive. This is because it works with abstractions (nodes, relationships, etc.) that fit the domain better. But I think the most important difference in this case appears when it’s time to evolve the code. How do you change the traversal depth in the SQL solution? How to change the traversal depth dynamically depending on facts found in the attributes/features?
Conclusion
It should be noted that the examples above are all very trivial. When dealing with real-world problems differences that may seem small from the tiny code examples could prove to have a strong impact. Also, I didn’t mention performance so far, but in many cases this could be the main reason to move graph data to a native graph database.
What is actually the root cause of the differences between relational databases and graph databases outlined in this article? It lies in a fundamental difference in design of the underlying data models. The relational model is based on the assumption that database records are what primarily matters while relationships between records come second place.
Graph databases instead assume that the relationships are as important as the records. This difference has numerous consequences for ease of use as well as for performance. A table-based system makes a good fit for static and simple data structures, while a graph-based fits complex and dynamic data better.
What actually matters in your data? Think about it!
Update 2009-09-21: changes to the you-might-know code and description
Want to learn more about graph databases? Click below to get your free copy of O’Reilly’s Graph Databases and get started building your own graph database application today.















