Did You Take the Neo4j 5 Cypher Bullet Train?

Field Engineer, Neo4j
6 min read

How to make your queries 1000x faster with quantified path patterns (QPP)
Motivation
If you take a look at Neo4j 5 release notes and do search for “cypher”, you’ll find 48 matches. Still counting. And you will see many new features and enhancements of our favorite query language.
To make evidence of the relevance of these improvements, we will do a case study using two of them:
- the Neo4j 5.0+ COUNT{<subquery>} syntax
- and the Neo4j 5.9+ ability to make Graph Pattern Matching with Quantified Path Patterns.
We could have also found an example leveraging EXISTS{<subquery>} syntax, predicates involving labels and types, and many more.
Are these features and enhancements worth the effort of upgrading your instances or refactoring your queries? Let me try to give an answer to this question, focusing on a standard fraud detection query use case.
We will compare, in a real use case, the performance of two queries doing the same job. The second is the one leveraging Neo4j 5 new features.
Use Case: Transaction Fraud Ring
According to the previously cited documentation, a transaction fraud ring refers to a group of people collaborating to engage in fraudulent activities, like transferring funds through multiple accounts.
They try to hide their tracks in the multitude of transactions, but when you take a step back, you see these patterns of people hiding their money flows pop out again from the regular transactions graphs.
These rings work across different locations and employ diverse strategies to evade detection. It is critical for financial organizations to detect these rings, especially with enhancement to the Contingent Reimbursement Model (CRM). One of the fastest-growing scams is the Authorized Push Payment (APP) fraud. In the UK, according to UK Finance, it resulted in a loss of over £249 million in the first half of 2022, a 30% increase compared to the same period in 2020.
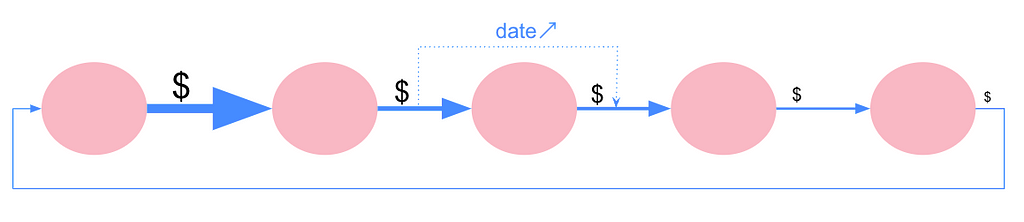
To detect these frauds, we have to find non-repeating chronologically ordered cycles inside a graph of transactions between accounts. From one transaction of this cycle to the next one, a slice of the amount (up to 20%) may be taken by the account. It looks like a great use case for pattern matching with Cypher query language.
Good Old Cypher

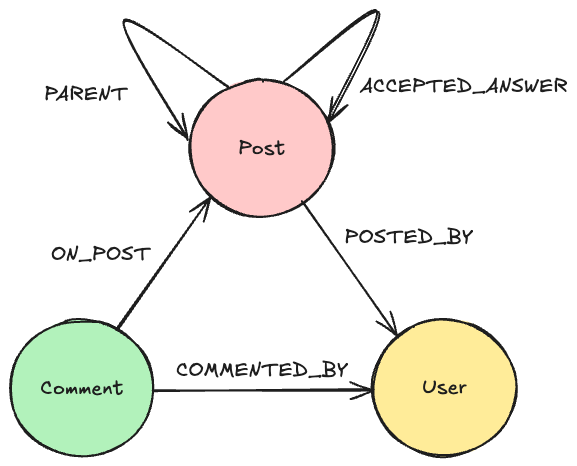
Before Neo4j 5, deep traversal queries were easier to write and run against a monopartite graph. A monopartite graph contains a single set of nodes. In Neo4j terms, it means we have nodes with a single label.
That’s why an (:Account)-[:TRANSACTION]->(:Account) model used to be the recommended way of modeling this use case.
Here is the query a skilled Cypher developer would have written some months ago:
When we PROFILE this query to analyze the query plan, we see it is computed in a traverse, produce, and filter fashion. All possible paths matching the coarse pattern are produced and pipelined to the filtering part of the process.

Better Neo4j 5 Cypher
With Neo4j 5, we have better options.
COUNT{<subquery>}
First of all, we can use the COUNT{<subquery>} to compute what was (possible but) hard to do without APOC before. Thanks to this opportunity, the Neo4j 5 query we are building will have no dependency on APOC. Cypher is getting more expressive and concise, and that’s great news! So, let’s tackle this query in pure Cypher Language.
Quantified Path Patterns
The second opportunity to refactor this query is the use of Neo4j 5.9+ Quantified Path Patterns (QPP).
Quantified Path Patterns can be seen as regular expressions of graph patterns. Consider reading Finbar Good’s blog to get a deeper insight into QPPs.
Getting From Denmark Hill to Gatwick Airport With Quantified Path Patterns
They enable us to describe complex patterns with precision, in a multipartite graph environment. That’s why we don’t need to stick to a monopartite model anymore. Let’s use this bi-partite model:
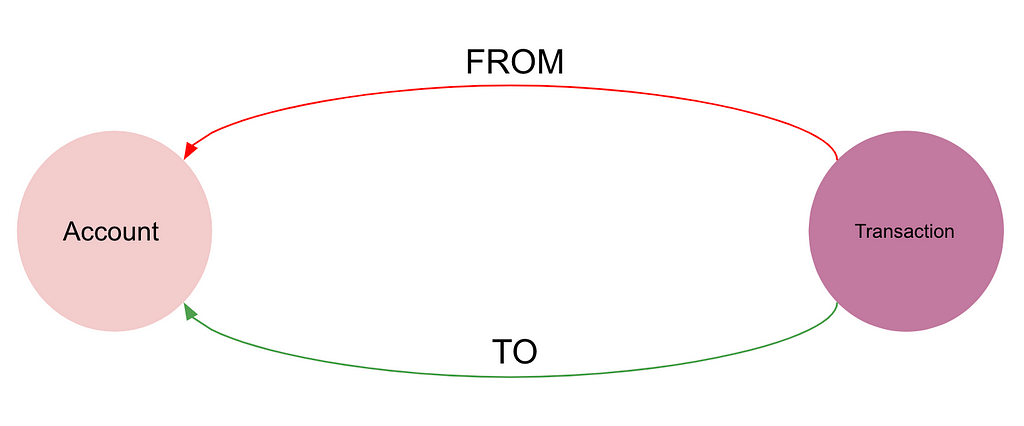
QPPs will also give us the ability to apply locally defined rules to filter the path we produce sooner in the process, avoiding the production of many useless rows. This gives us great confidence that we won’t need to cap the length of the path like we did in the previous version.
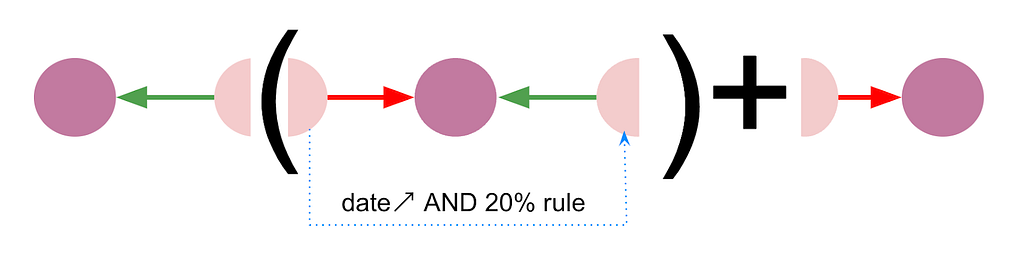
Here is how our previous query translates into Neo4j 5 fancy Cypher :
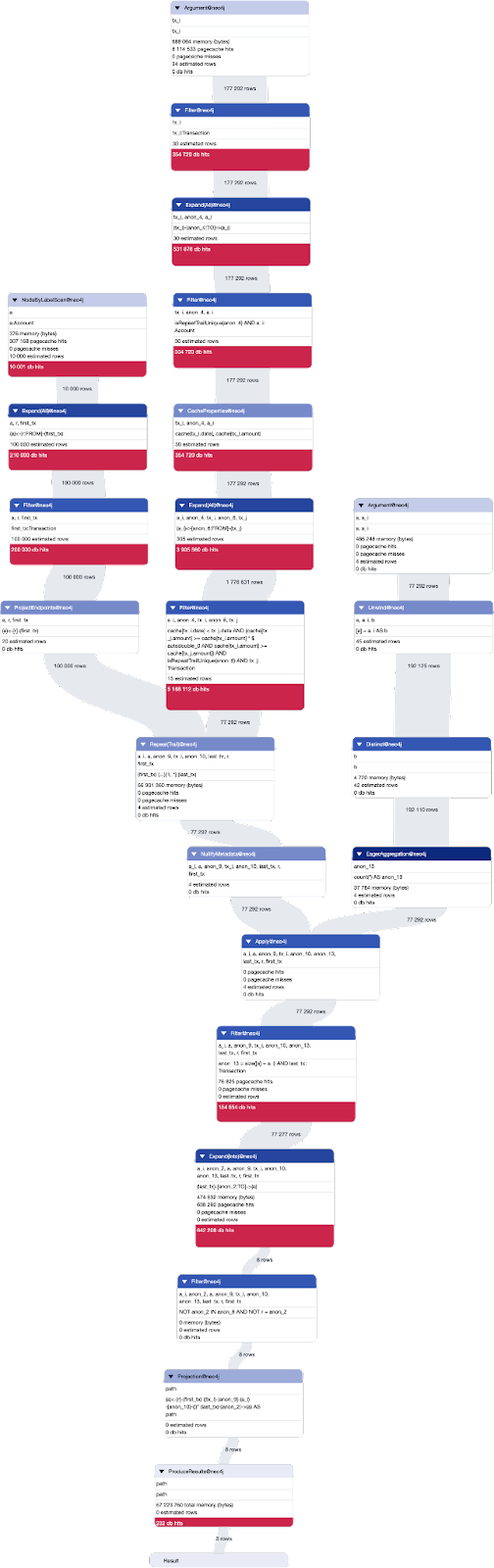
The PROFILE of our query is way less linear. If there were only one thing to notice, it would be this one: there is a Filter computing step planned upstream to the Repeat processing step.

This means that our transaction graph is traversed using only date-consistent and 20%-rule-compliant steps. This reduces in a drastic way the search space our pattern-matching engine has to go through.
Let’s compare performances.
Benchmark
This benchmark can be reproduced by following the first half of this tutorial (sprint 1 and 2).
fraud-detection-training/README.md at main · halftermeyer/fraud-detection-training
Performance
We’ll use a small auraDB instance with this setup for benchmarking:
Neo4j 5, 1GB of memory, 2GB of storage, and 1 CPU.

Let’s run both queries to compare performance on the same dataset containing 10,000 accounts and 100,000 transactions.
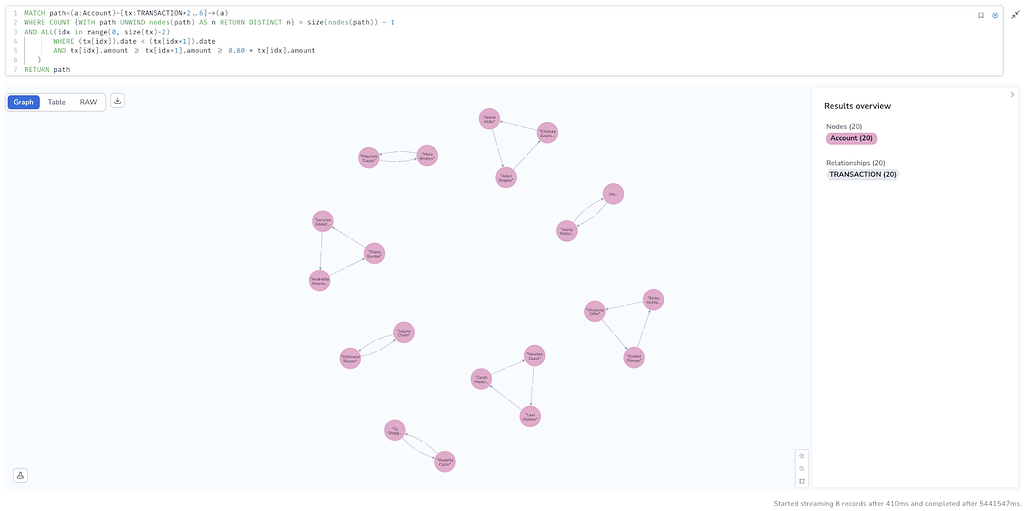
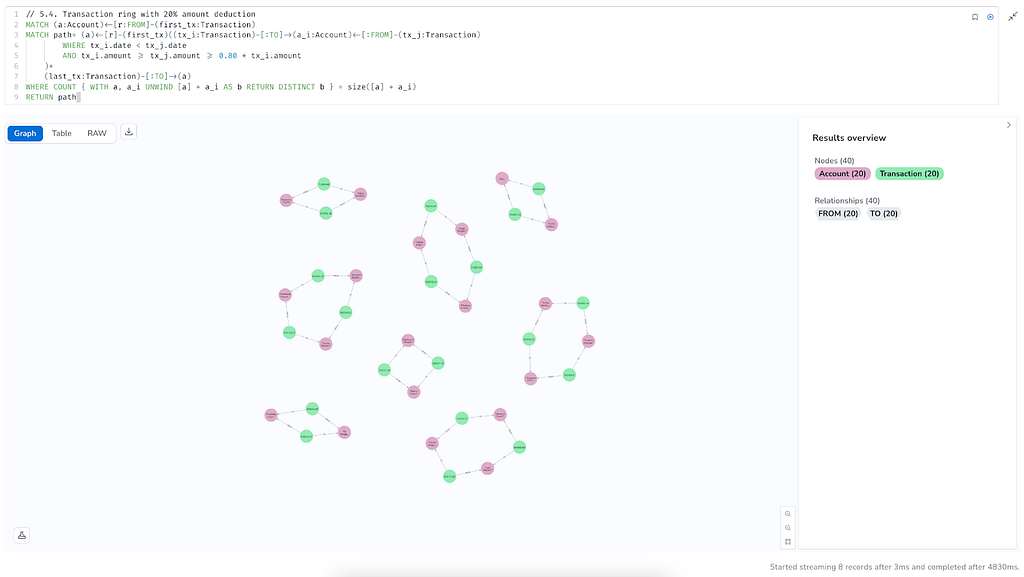
The first thing we notice is that both queries return the same 8 results. That’s a good starting point for performance benchmarking.
Let’s now zoom in to see the response time for both queries.
For the good old Cypher query on the monopartite model:

For the QPP-based Neo4j 5 Cypher query on the bipartite model performed :

Almost 2 hours on one side and less than 5 seconds on the other. For the same job and the same result (but with no guarantee of exhaustivity for the first one, because of the length cap). You would probably already agree such a 1000x query time factor is impressive! But it’s not over yet.
Exhaustivity
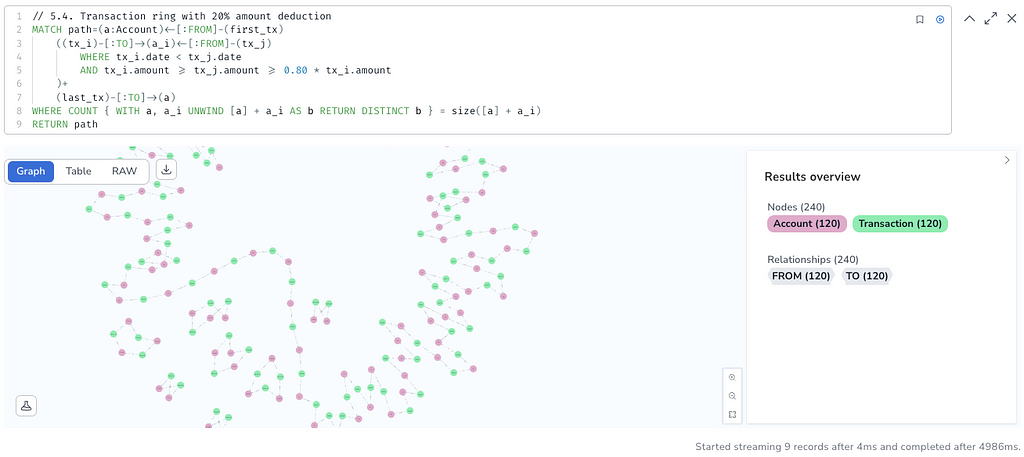
We now add a 100-hop cycle to our dataset to challenge our queries.
The first query would need a huge amount of memory and time to run in such a connected environment with no pattern length limit. Indeed, as the average outgoing degree is 10 in our dataset, with a pattern length limit set to 6, the pattern-matching step of the query produces 10 to the 6th rows (1,000,000 rows). To capture 100-hop cycles, we would need to produce 10 to the 100th rows. This number is one hundred billions of billions times greater than the number of atoms in the universe. So we won’t.
By contrast, the second query does. It returns the 100-hop-long 9th cycle in 5 seconds. Our QPP-based query scales just fine!
Insights
Such an improvement may have different value for you, depending on where you’re at on your journey with Neo4j.
It may mean you should refactor some analytical queries of yours into real-time transactional ones.
Or maybe something you thought last year was impossible to compute is now one upgrade and one QPP away from what you already have.
But in all cases, you should definitely consider boarding the Neo4j 5 bullet train.
Did You Take the Neo4j 5 Cypher Bullet Train? was originally published in Neo4j Developer Blog on Medium, where people are continuing the conversation by highlighting and responding to this story.