A New Way of Looking at “Moving Relationships” in Neo4j

Learn Why You Should Understand “Moving Relationships,” a New Kind of Data Relationship in Neo4j

[As community content, this post reflects the views and opinions of the particular author and does not necessarily reflect the official stance of Neo4j.]

Introduction

A graph database is not only a simple way to store connected data, it is also a powerful tool to manage dynamic relationships between data.

Since relationships are natively implemented in Neo4j, we can use them as a simple way to identify a group of connected nodes. But it is not the only usage we can make of them.

There are many use cases where consecutive queries can move the relationships between nodes. These relationships are intended to store a particular state for a sub graph like a pointer for example. Let’s have a closer look.

Relationship as a Pointer

To observe this behavior, our first example is the famous Linked List. A linked list is a list where each item is ordered according to its relative position compared to the others items.

On each call, the currently pointed element is returned and then the pointer moves to the next element (like in Java with the Iterator object iterator ().next () ).

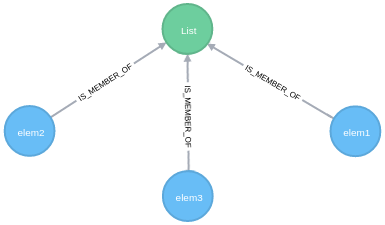
First we need to create a :LIST node with three :ELEMENT nodes linked to it.

MERGE (elem1:ELEMENT{name:"elem1"})-[:IS_MEMBER_OF]->(list:LIST{name:"List"})
MERGE (elem2:ELEMENT{name:"elem2"})-[:IS_MEMBER_OF]->(list)
MERGE (elem3:ELEMENT{name:"elem3"})-[:IS_MEMBER_OF]->(list)

Figure 1. The list with elements

Then we need to link these elements in a relative ordered way. (The initial position is not necessarily important. We chose here to match elements alphabetically ordered by their name property) :

    MERGE (elem:ELEMENT)-[r:IS_MEMBER_OF]->(list:LIST)
    WITH elem ORDER BY elem.name ASC
    WITH COLLECT(elem) AS elems
    FOREACH (n IN RANGE(0, LENGTH(elems)-2) |
    FOREACH (prec IN [elems[n]] |
    FOREACH (next IN [elems[n+1]] |
    MERGE prec-[:NEXT]->next)))

Figure 2. Linked elements

Here we use a loop (the first FOREACH clause) to browse the collection of elements and to create a relationship between the previous node and the next node.

If you need more explanations about this query, you can find a very interesting post from Mark Needham here: Neo4j: Cypher – Creating relationships between a collection of nodes.

The next step consists in placing a pointer at the initial position, meaning on the header element of this list (the element without a :NEXT incoming relationship):

    MATCH (list:LIST)
    MATCH (elem:ELEMENT) WHERE NOT elem<-[:NEXT]-()
    MERGE list-[:POINTER]->elem

Figure 3. Initial position of the pointer

Now, we have to write a typical query which returns the current pointed element and emulates the pointer movement.

Returning the current element is simple :

    MATCH (list:LIST)-[:POINTER]->(current:ELEMENT) 
    RETURN current

But emulating the pointer movement requires three Cypher operations :

Finding the next node
Deleting the current pointer relationship
Creating a new pointer relationship on the next node

The final query is:

    MATCH (list:LIST)<-[:IS_MEMBER_OF]-(elems:ELEMENT)
    MATCH (list)-[p:POINTER]->(current:ELEMENT) 
    MATCH current-[:NEXT]->(next:ELEMENT) 
    DELETE p 
    MERGE list-[pnew:POINTER]->next
    RETURN DISTINCT list,current,next,pnew,elems

Figure 4. First move of the pointer

The pointer moved!

If we take five minutes to have a closer look at the type of the relationships, we have:

:IS_MEMBER_OF to determine what the elements of this list are
:NEXT to determine what the next element to the current one is
:POINTER to determine what the current element is

As we can see, the nature of each relationship type is different. The first two ones have a long lifecycle (as long as the list exists) and the last one has another function: its lifetime may be short because it is only a volatile state at any given moment.

This is a moving relationship!

Relationships as a Three-Way Switch

Yes, it is a weird title and a strange use case. I think that it is interesting to introduce another way of thinking about data relationships.

Previously we were talking about a relationship as a pointer, now we have to consider combined states. And the best example to introduce this notion is the electrical three-way switch.

In the hallway of your house, you need to switch the light on or off from more than one location. You have to be able to switch the light on from the entrance (front switch) and to switch it off from the other end (rear switch), since it wouldn’t make sense to turn the light on only from the last place where you turned it off.

In the domain of electricity such a switch is called a three-way switch, and its implementation is as follows:

Figure 5. A three-way switch. Image source.

Very well, but what is the link with graphs?

In the domain of electricity, switching the light on requires a closed circuit. In graph theory, a closed circuit is called a cycle, meaning that it should be possible to easily convert it into a graph.

If we can detect a cycle through these elements we can deduct that the lamp is on, whereas if we cannot find a closed cycle, the light remains off.

First, we need to represent this schema in Neo4j, and we consider that the initial position is when the light is off:

    CREATE 
    (generator:GENERATOR {name:"generator"}),
    (lamp:LAMP {name:"lamp"}),
    (s1:SWITCH {name:"front-switch"}),
    (e11:ENDPOINT {name:"front-endpoint-1"}),
    (e12:ENDPOINT {name:"front-endpoint-2"}),
    (s2:SWITCH {name:"rear-switch"}),
    (e21:ENDPOINT {name:"rear-endpoint-1"}),
    (e22:ENDPOINT {name:"rear-endpoint-2"}),
    generator-[:TO]->lamp,
    lamp-[:TO]->s2,
    s2-[:POINTER]->e22,
    e22-[:TO]->e12,
    generator<-[:TO]-s1,
    e11-[:POINTER]->s1,
    e11<-[:TO]-e21

Figure 6. The first adaptation.

The TO relationships represent the electrical wires.
The POINTER relationships represent the current states of the switches.

But this graph isn’t sufficient, because we can’t find the next Endpoint from the currently pointed position. We need to build a circular linked list around the endpoints for each switch.

Here is the query for the rear switch:

    MATCH (s2:SWITCH {name:"rear-switch"})
    MATCH (endpoint:ENDPOINT) WHERE endpoint.name=~"rear.*"
    MERGE endpoint-[:IS_A_PART_OF]->s2
    WITH endpoint ORDER BY endpoint.name ASC
    WITH COLLECT(endpoint) AS elems
    FOREACH (n IN RANGE(0, LENGTH(elems)-2) |
    FOREACH (prec IN [elems[n]] |
    FOREACH (next IN [elems[n+1]] |
    MERGE prec-[:NEXT]->next)))
    WITH elems[0] as beginning, elems[LENGTH(elems)-1] as ending
    MERGE beginning<-[:NEXT]-ending

And here is the query for the front switch:

    MATCH (s1:SWITCH {name:"front-switch"})
    MATCH (endpoint:ENDPOINT) WHERE endpoint.name=~"front.*"
    MERGE endpoint-[:IS_A_PART_OF]->s1
    WITH endpoint ORDER BY endpoint.name ASC
    WITH COLLECT(endpoint) AS elems
    FOREACH (n IN RANGE(0, LENGTH(elems)-2) |
    FOREACH (prec IN [elems[n]] |
    FOREACH (next IN [elems[n+1]] |
    MERGE prec-[:NEXT]->next)))
    WITH elems[0] as beginning, elems[LENGTH(elems)-1] as ending
    MERGE beginning<-[:NEXT]-ending

Note that the last query line MERGE beginning<-[:NEXT]-ending is useful to link the last element to the first and thus to obtain a circular reference.

Figure 7. The second adaptation.

Lamp test query:

    MATCH (lamp:LAMP)-[r:TO|POINTER*]->(g:GENERATOR) RETURN lamp

No result here (the lamp is off), meaning the path is broken since a TO or POINTER relationship is missing:

Figure 8. A broken path.

When a user toggles the rear switch to turn on the light, it triggers the query below.

Toggling the rear switch query:

    MATCH (s2:SWITCH{name:'rear-switch'})-[p:POINTER]->(current:ENDPOINT) 
    MATCH current-[:NEXT]->(next:ENDPOINT) 
    DELETE p 
    MERGE s2-[pnew:POINTER]->next
    RETURN s2,current,next,pnew

Figure 9. Touching the rear switch.

The rear switch pointer moves from its initial position to the second one and thus closes the path between the lamp and the generator.

Now let us test the lamp with this query:

    MATCH (lamp:LAMP)-[r:TO|POINTER*]-(g:GENERATOR)-[r2:TO]-(lamp) RETURN DISTINCT lamp

The light is on!

Figure 10. A closed path.

The result would be the same with the front switch, since we emulated a three-way switch.

It is a good starting point for home automation applications, isn't it? Imagine a graph that stores all the positions of lamps, doors, gates or shutters of your house...and then, more complex graphs to manage an entire building (i.e., facility management)!

You can also try to obtain the same results in SQL, but I expect this to be challenging.

Note that our representation is simplified on purpose. A switch could be modeled using a pre-defined component with three endpoints (one input and two outputs). If so, we could model a graph composed of combinations of components (with internal states) rather than composed of combinations of unitary nodes, but that is another story.

Conclusion

As we can see, there are different natures of data relationships: Some of them have a permanent life, like the electrical wires in our previous example; some of them, like pointers, have a lifecycle and are supposed to store a state. The latter are the ones I call moving relationships.

Special thanks to Patricia for reviewing.

Editor's note: Sylvain Roussy is also the author of the French ebook introduction to graph databases and Neo4j, and he'll be publishing a new edition in December with an update for Neo4j 2.3.

Want to learn more about graph databases? Click below to get your free copy of O’Reilly’s Graph Databases ebook and discover how to use graph technologies for your mission-critical application today.

Download My Free Copy