A Cypher Game of Life

In the early spring of 2025, we will see the release of the next major version of Cypher, the query language of Neo4j. This will be called Cypher 25. One new feature in the first release will be conditional queries. I wanted to write a blog for that feature, and I needed a use case for it, so I decided to do a Cypher implementation of Conway’s Game of Life. I wrote the entire blog, feeling fairly good about it, when I suddenly realized that I could do the query in a much nicer way without using conditional queries.

Imagine the despair! Here I was with a blog that I felt good about, but with the main purpose of it lost (all because this darn language is too good). And just when I thought all hope was lost, I saw this competition posted by my colleague Jon Giffard with a challenge to write Game of Life in GraphQL. I decided to go ahead with my post on Game of Life as a hint on how it can be solved in a different language. As we’ll see, Cypher is ideal for this problem.

By the way, I did come up with another example to show the use of conditional queries, so that blog will still come. It’ll be published with the release of Cypher 25 later this spring.

Conway’s Game of Life

Conway’s Game of Life is a cellular automaton invented by British mathematician John Horton Conway in 1970.

In Game of Life, you have a game board (grid) with X number of columns and Y number of rows. Each cell in the grid can either be alive (normally illustrated by a black square) or dead (white square). Each cell (except those on the edge of the game board) has eight neighbors (above, below, to the left, to the right, and diagonally).

For each generation (tick), a cell can either be born, die, or remain (dead or alive). What happens to the cell depends on the number of living neighbors. If there are too few neighbors, it will die of loneliness; if there are too many, it will die of starvation. The following table describes what happens to a cell under different conditions:

Number of living neighbors  Living cell    Dead cell
≤1                          Dies           Remains dead
2                           Stays alive    Remains dead
3                           Stays alive    Is born
≥4                          Dies           Remains dead

This means that if a living cell has two or three living neighbors, it stays alive, otherwise it dies. If a dead cell has three living neighbors, it is born (or reborn).

So if we have a game board of 5*5 cells and start with this initial state:

After one tick it would be:

And after yet another tick:

The Implementation

You might almost think that Conway was a Cypher expert when he devised his game, but given that it was more than 40 years before Cypher was invented (even before SQL came to be), and given the lack of time machines, that seems unlikely. Still, it’s an algorithm that seems incredibly well suited for Cypher.

One tricky part when implementing this in a traditional language like Java is that all events in one tick are mountainous. This means that if a cell is born, it shouldn’t be counted as born when you go on to evaluate its neighbor. One solution is to have a copy of the game board where you create the new state and you switch that to be the current state.

But in a declarative language like Cypher, we don’t have to think about that, which makes it ideal for this task. When we have a MATCH followed by a write operation like SET, the subsequent write will not affect the preceding MATCH.

Java Implementation

Let’s look at what a Java implementation could look like using a hard-coded initial state (the example from previous section):

public class ConwaysGameOfLife {
  private static final int TICKS = 2;
  private static final int WIDTH = 5;
  private static final int HEIGHT = 5;
  private static final int[][] INITIAL_STATE = {{2,1},{1,2},{2,2},{3,2},{1,3},{3,3},{2,4}};
  
  private final int width;
  private final int height;
  private boolean[][] gameBoard;
  
  public ConwaysGameOfLife(int width, int height, int[][] initialState) {
    this.width = width;
    this.height = height;
    
    gameBoard = new boolean[width][height];
    
    for (int[] cell : initialState) {
      gameBoard[cell[0]][cell[1]] = true;
    }
  }
  
  public void tick() {
    boolean[][] newState = new boolean[width][height];
    
    for (int y = 0; y < height; y++) {
      for (int x = 0; x < width; x++) {
        int neighbours = countNeighbours(x, y);
        if (neighbours <= 1 || neighbours >= 4) {
          newState[x][y] = false;
        }
        else if (neighbours == 3) {
          newState[x][y] = true;
        }
        else {
          newState[x][y] = gameBoard[x][y];
        }
      }
    }
    
    gameBoard = newState;
  }
  
  private int countNeighbours(int x, int y) {
    int neighbours = 0;
    for (int yy = Math.max(y-1, 0); yy <= Math.min(y+1, HEIGHT - 1); yy++) {
      for (int xx = Math.max(x-1, 0); xx <= Math.min(x+1, WIDTH - 1); xx++) {
        if ((xx != x || yy != y) && gameBoard[xx][yy]) {
          neighbours++;
        }
      }
    }
    return neighbours;
  }
  
  public void printState() {
    for (int y = 0; y < height; y++) {
      for (int x = 0; x < width; x++) {
        System.out.print(gameBoard[x][y] ? "X" : ".");
      }
      System.out.println();
    }
  }

  public static void main(String[] args) {
    ConwaysGameOfLife game = new ConwaysGameOfLife(WIDTH, HEIGHT, INITIAL_STATE);
    
    for (int i = 0; i < TICKS; i++) {
      game.tick();
    }
    
    game.printState();
  }
}

It’s probably easy to write both a more efficient and a better-structured implementation, but we still see how verbose it gets in Java. Counting neighbors and managing double states are things made a lot simpler in Cypher.

Cypher Implementation

For a Cypher implementation, we will have our game board in our database as a graph. It will be a graph of nodes called Cell, and each with a NEIGHBOR relationship to all eight neighbors (we don’t care about the direction).

The first thing we need for our tick query is to count the number of neighbors for each cell in the grid. As we see in the Java routine, we needed one nested for-loop to go through all cells and another nested for-loop to count the number of neighbors for each cell. In Cypher, we achieve both with three lines of code:

MATCH (cell:Cell)
OPTIONAL MATCH (cell)-[:NEIGHBOUR_OF]-(:Cell {alive: true })
WITH cell, COUNT(*) AS liveNeighbours

Now we need to update the state of the cell based on this. This is where I thought I’d show conditional queries, but I realized it was solved much more efficiently with case expressions:

SET cell.alive =
CASE liveNeighbours
  WHEN <= 1 THEN FALSE
  WHEN >= 4 THEN FALSE
  WHEN = 3 THEN TRUE
  ELSE cell.alive
END

And that’s all we need for our tick implementation.

Full Implementation in Cypher

To make it comparable to the Java version, we need to include setting up the initial state, printing the result, etc. First, we’ll delete any previous game we may have in our database:

MATCH (c:Cell) DETACH DELETE c

Then we can define our parameters for the initial state (same as used in the Java version):

:param {
  height: 5,
  width: 5,
  cells: [[2,1],[1,2],[2,2],[3,2],[1,3],[3,3],[2,4]]
}

Now let’s create the game board as the graph in the image in previous section. We’ll include a coordinate in each cell so we can visualize the graph later:

UNWIND range(0,$height-1) AS row
WITH row
UNWIND range(0,$width-1) AS column
WITH row, column
CREATE (cell:Cell {coordinate: Point({x:column,y:row}), alive:false})
WITH row, column, cell
UNWIND [[row-1, column-1],[row-1, column],[row-1, column+1],[row, column-1]] AS neighbor
MATCH (other:Cell {coordinate: Point({x:neighbor[1],y:neighbor[0]})})
MERGE (other)-[:NEIGHBOUR_OF]->(cell)

Then we’ll set the initial state:

UNWIND $cells AS cell
MATCH (c:Cell {coordinate: Point({x:cell[0],y:cell[1]})})
SET c.alive = true

Now we have everything set up. With that, we’ll just run the tick query (the same as we worked with previously) as many times as we want to tick. To follow the same example, we should tick twice (i.e., run this query twice):

MATCH (cell:Cell)
OPTIONAL MATCH (cell)-[:NEIGHBOUR_OF]-(:Cell {alive: true })
WITH cell, COUNT(*) AS liveNeighbours
SET cell.alive =
CASE liveNeighbours
  WHEN <= 1 THEN FALSE
  WHEN >= 4 THEN FALSE
  WHEN = 3 THEN TRUE
  ELSE cell.alive
END

Finally, we want to be able to print our state. We can print our state as ASCII, with X as live cells and . as dead cells, just like we did in the Java version:

MATCH (cell:Cell)
WITH cell ORDER BY cell.coordinate.y ASC, cell.coordinate.x ASC
WITH collect(cell) AS cells
RETURN reduce(
  res = "",
  cell IN cells | 
  res + 
    CASE cell.coordinate.x = 0
      WHEN true THEN "\n"
      ELSE ""
    END +
    CASE cell.alive 
      WHEN true THEN "X" 
      ELSE "."
    END) AS result

You may notice we always print an empty line before outputting the actual lines. This makes it look better when run in the Neo4j Query tool. This tool starts with a quotation mark, and by starting with an empty line, we get our lines better aligned since we don’t get the first line indented by the quotation mark.

"
..X..
.X.X.
XX.XX
.X.X.
..X.."

A Graphical Version

Now we have something comparable between Java and Cypher that both outputs the ASCII state after a number of ticks. But wouldn’t it be nice with a graphical output that updates every time we tick? In Java, we could do that by creating a JFrame and rendering the state there. It would require quite a bit more code, but wouldn’t be too difficult. But could we do it with Neo4j?

A while ago, I wrote a blog about rendering the Mandelbrot fractal in Cypher. There, I also produced the result in ASCII art. But a colleague mentioned that I could have used Neo4j Bloom to get a semi-graphical output, which I tried with a very impressive result.

I’ve been using Aura Free for these experiments so far, and let’s stay there. It’s free, includes Bloom, and is more than enough for the small graphs we use here. If you don’t already have an instance, you can go to the link above, register with your Google account, and create a free instance.

All the queries I ran in the previous section were run in the tool called Query, which you access here in the console:

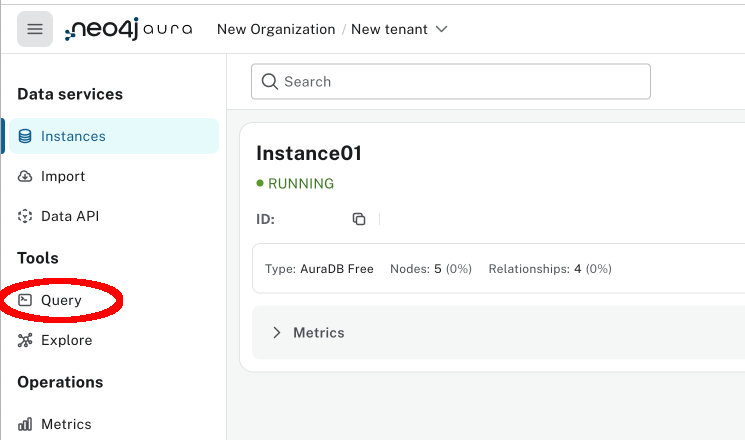
In that tool, you can just paste all the queries listed in the previous section, in the same order, and you should get the same results.

We said we wanted to use Bloom now, but before we head over there, let’s stay in Query and set everything up. Run all the queries in the previous chapter until you get to the tick query (don’t run that one). You should have the game board and the initial state set up.

Now we can head over to Bloom. In the console, it’s called Explore and is the option just below Query in the toolbar.

You’ll see an empty workbench. At the top, you see the Perspective path (Perspectives/Default Perspective). To the right of that, there’s a book-shaped icon. Click it.

In this new toolbar that pops up, click on the Saved Cypher option on the far right. Now click Add Search phrase. In the new dialog, add “Show all cells” as both Search phrase and Description, and for Cypher query, you enter:

MATCH (c:Cell) RETURN c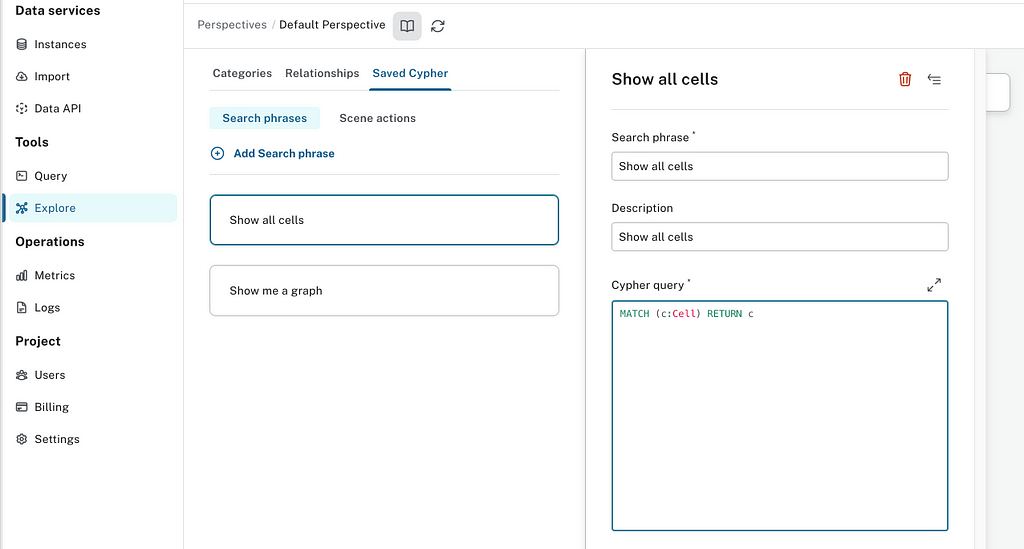

Now add one more search phrase. Call this one “Tick” and use the entire tick query from above, but with a RETURN cell at the end:

MATCH (cell:Cell)
OPTIONAL MATCH (cell)-[:NEIGHBOUR_OF]-(:Cell {alive: true })
WITH cell, COUNT(*) AS liveNeighbours
SET cell.alive =
CASE liveNeighbours
  WHEN <= 1 THEN FALSE
  WHEN >= 4 THEN FALSE
  WHEN = 3 THEN TRUE
  ELSE cell.alive
END
RETURN cell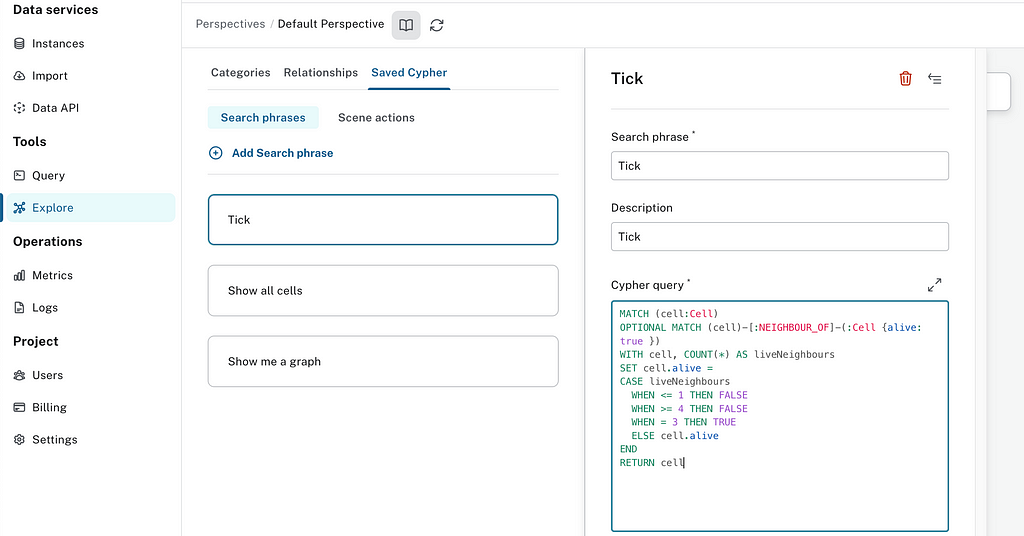

Now close down the Perspective designer (by clicking the book icon again). In the Search field, select Show all cells and click the execute button (the play icon). We now see all the cells of the game, but just in a random mess.

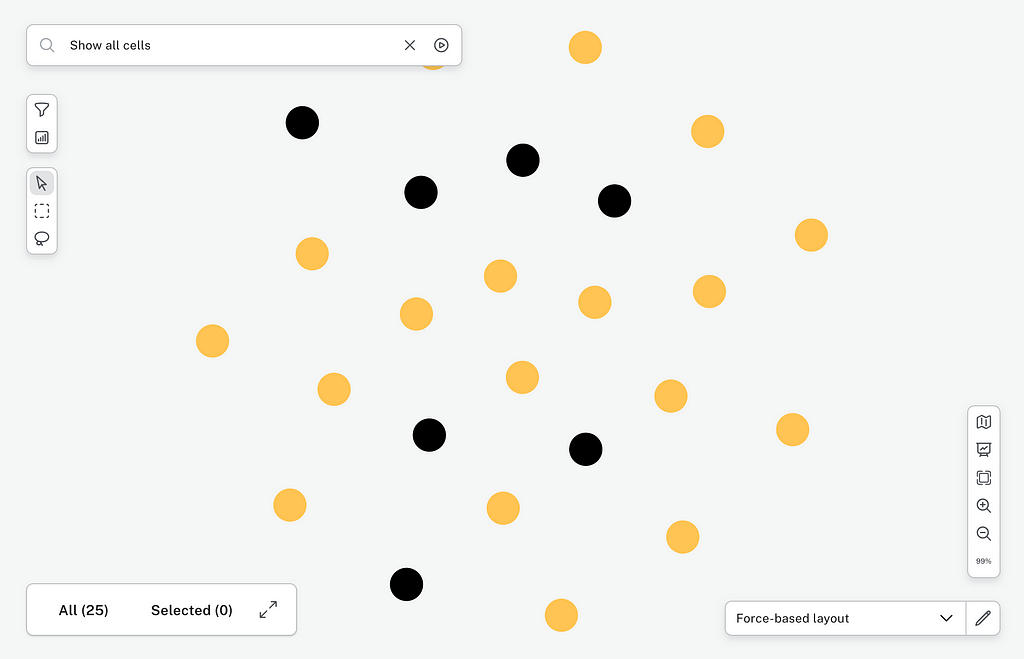
But since we added a property on each Cell called coordinate as a point holding the grid position of each cell, we can have Bloom understand how it should be laid out.

In the lower right corner, there’s a layout option that says Force-based layout. Click it and select Coordinate layout.

In the popup, we can define some options for how we want it laid out — specifically, the distance between nodes (by pulling the X and Y bars). I wanted the nodes a little closer together than they were by default.

All our cells are now orange (might be a different color in your case), but we want to see who is alive and who’s dead. And we don’t need the word Cell on each cell. To fix that, click on the circle next to the Cell label on the right-hand side of the screen. The circle would be the same color as what you currently have for the cells (orange in my case).

On the Color tab shown when the dialog appears, choose what color you want the dead cells to be. I’ll keep the orange color I got as default, but choose what you like.

Now click the Text tab at the top and uncheck all the boxes (for all the properties).

Once those are unchecked, click Rule-based on the top, click Add rule-based styling, select the alive property, select is true in the Select condition box, check the Apply color box, and select the color for living cells (I chose black).

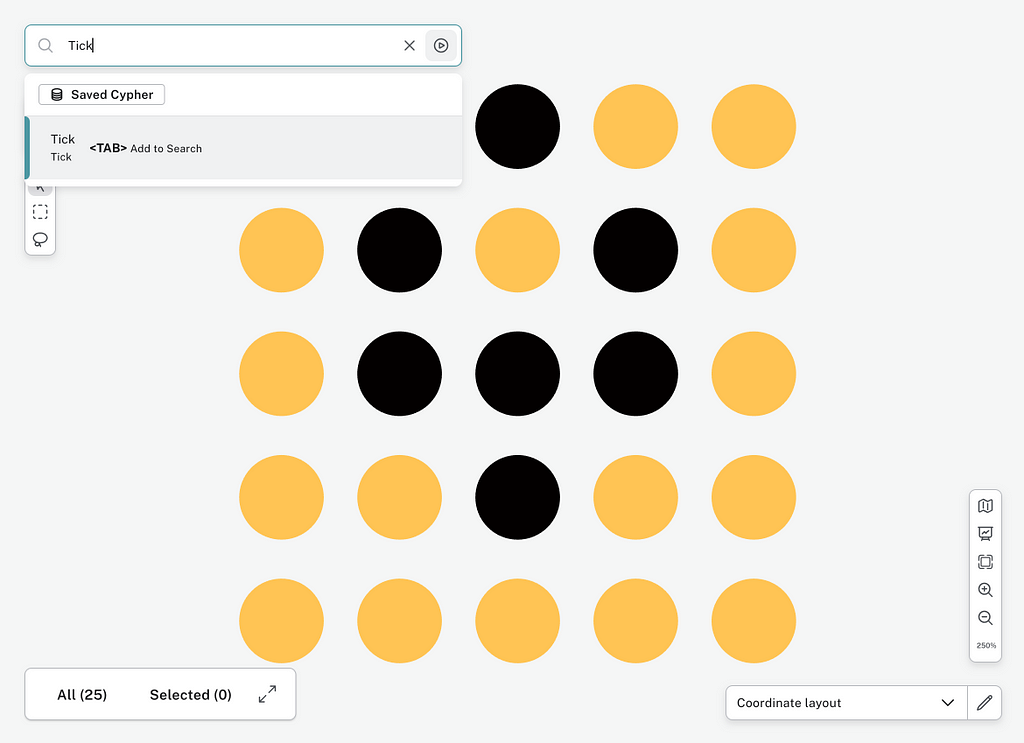
Now we see the color-coded Game of Life grid, although upside-down compared to how we viewed it before. This is because Bloom sees the Y coordinate as going upward (as in traditional charts) rather than downward (as traditional for computer screens).

Now we’re ready to tick the game and see the changes live. Just select Tick in the Search box, click the play icon, and you’ll see the game tick. Continue to click play over and over and see the game tick forward.

Gosper Glider Gun

So what’s the point of this? What is the point of a zero-player game? Well, the challenge is trying to conceive initial states that don’t die too quickly — and maybe even infinite games. If, at any point, the game comes back to the initial state, it will iterate forever. Some such patterns are called “Guns” because they emit spaceships or gliders from the main pattern, which repeats forever.

One of the first and most well-known guns was conceived in 1970 by Bill Gosper: the Gosper glider gun. This consists of two blocks* and two structures (“queen bee shuttles”) bouncing between the two blocks, emitting gliders periodically. The pattern repeats itself every 30 generations.

* A “block” is a pattern that doesn’t change from one generation to the next. The most common block is four cells arranged 2 by 2. Every cell alive has exactly three alive neighbors and will thus stay alive, while none of the dead cells surrounding it has three alive neighbors and, therefore, won’t be born.

If we want to test the Gosper glider gun in our Cypher implementation, we can use these parameters:

:param {
  height: 40,
  width: 40,
  cells: [[26,37],[24,36],[26,36],[14,35],[15,35],[22,35],[23,35],[36,35],[37,35],[13,34],[17,34],[22,34],[23,34],[36,34],[37,34],[2,33],[3,33],[12,33],[18,33],[22,33],[23,33],[2,32],[3,32],[12,32],[16,32],[18,32],[19,32],[24,32],[26,32],[12,31],[18,31],[26,31],[13,30],[17,30],[14,29],[15,29]]
}

If we do the setup and initialization routines from above using those parameters, then play it using the Bloom visualization we discussed, we get to view the Gosper glider gun in action like this:

Summary

There you have it. We have seen how efficient a cellular automaton implementation can be in Cypher, and we have also seen how to use Bloom as both an interactive and graphical tool for our automaton.

Be sure to check out Win a $250 Gift Card: Build Conway’s Game of Life With GraphQL for AuraDB Beta. And to learn more about Cypher, check out the Cypher Fundamentals course on GraphAcademy.

---

A Cypher Game of Life was originally published in Neo4j Developer Blog on Medium, where people are continuing the conversation by highlighting and responding to this story.