I Would Walk 500 Miles

Introducing repeatable elements in the Cypher query language

In this post, I’ll show how to use the new REPEATABLE ELEMENTS match mode to solve queries that we weren’t able to before, like finding circular patterns where one of the nodes only has one incoming/outgoing relationship.

Have a look at this graph:

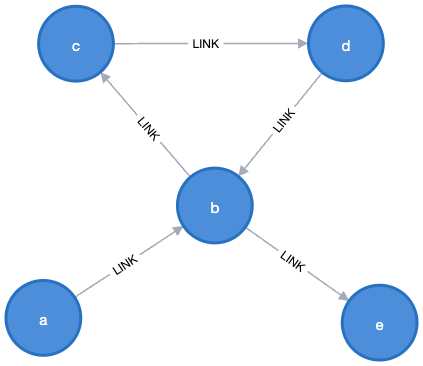
How many ways do we have of getting from a to e (following the direction of the relationships)? I think most of you would answer two, either directly through b, or with the detour through c and d.

Let’s try it out with Cypher:

MATCH p=(a {name: "a"})-->+(b {name: "e"}) RETURN p

And guess what? You were absolutely correct. We get two results:

(a)-[:LINK]->(b)-[:LINK]->(e)
(a)-[:LINK]->(b)-[:LINK]->(c)-[:LINK]->(d)-[:LINK]->(b)-[:LINK]->(e)

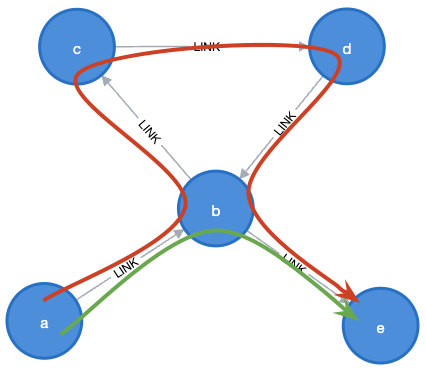
Well. Why wouldn’t this also be a solution?

(a)-[:LINK]->(b)-[:LINK]->(c)-[:LINK]->(d)-[:LINK]->(b)-[:LINK]->(c)-[:LINK]->(d)-[:LINK]->(b)-[:LINK]->(e)

or this?

(a)-[:LINK]->(b)-[:LINK]->(c)-[:LINK]->(d)-[:LINK]->(b)-[:LINK]->(c)-[:LINK]->(d)-[:LINK]->(b)-[:LINK]->(c)-[:LINK]->(d)-[:LINK]->(b)-[:LINK]->(e)

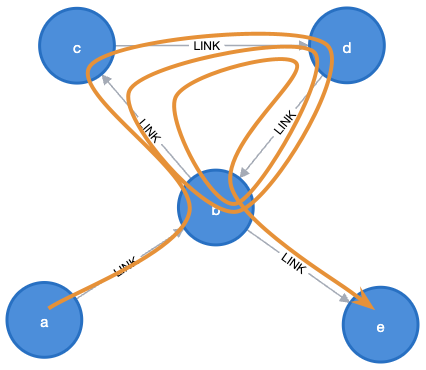
Because you can’t traverse the same relationship twice. We can only do one loop through c and d, but why? We could visit the same b node twice, so why not a relationship?

In Cypher, it has traditionally been allowed to revisit nodes, but not relationships, when you walk around the graph. This is called the DIFFERENT RELATIONSHIPS match mode, though you never had to think about that since it was the only supported one.

There are several reasons why DIFFERENT RELATIONSHIPS has been the default. It seems to be what we humans expect (consider the example above), but it is also less prone to infinite loops and has a lower computational cost.

However, with the new Cypher 25 version and the latest release of Neo4j, 2025.06.0, there will be a new match mode added called REPEATABLE ELEMENTS, which allows revisiting relationships as well. DIFFERENT RELATIONSHIPS is still default, but you can add the keyword REPEATABLE ELEMENTS after the MATCH:

MATCH REPEATABLE ELEMENTS <PATH PATTERN>, <PATH PATTERN>...

But why on earth would you ever want to do that? When would that ever be useful? Let’s have a look at a number of use cases.

The Dataset

For this, I wanted a dataset with all airports in the world and how they’re connected. I consider one airport connected to another if there is at least one airline operating that route with a regular flight. There will only be one connection at most between any two airports, and I don’t care about the direction (I assume that if an airline flies in one direction, they also fly in the other, which may be a simplification that isn’t always true, but at least in most cases).

I found that Jonty Wareing maintains a dataset of most airports and routes on GitHub, and we can write a Cypher query that imports that directly into a Neo4j database in the format I described above. This query is designed to also work in AuraDB Free:

MATCH (n) DETACH DELETE n;

CREATE INDEX iata IF NOT EXISTS FOR (a:Airport) ON (a.iata);

CALL apoc.load.json("https://raw.githubusercontent.com/Jonty/airline-route-data/refs/heads/main/airline_routes.json", null, {failOnError:false}) YIELD value
UNWIND keys(value) AS iata
WITH value[iata] AS iata
CALL(iata) {
  MERGE (airport:Airport {iata: iata['iata']})
  SET airport.location = point({latitude: toFloat(iata['latitude']), longitude: toFloat(iata['longitude'])})
  WITH iata, airport
  CALL(iata, airport) {
    UNWIND keys(iata) AS prop
    FILTER prop <> 'routes' AND prop <> 'iata' AND prop <> 'latitude' AND prop <> 'longitude'
    SET airport[prop] = iata[prop]
  }
  CALL(iata, airport) {
    UNWIND iata['routes'] AS route
    UNWIND route['carriers'] AS carrier
    WITH route, collect(carrier['name']) AS carriers
    MERGE (destination:Airport {iata: route['iata']})
    MERGE (airport)-[c:CONNECTION]-(destination)
    ON CREATE
    SET c += { km: route['km'], carriers: carriers } 
  }
} IN TRANSACTIONS OF 1000 ROWS;

Note the FILTER keyword in the query above. That’s another new feature in Cypher 25, which simply combines a WITH with a subsequent WHERE.

If you’re in Aura, you can run this in the Query tool. To visualize it, you can switch over to the Explore tool in the toolbar. Make sure the setting allows for at least 4,000 nodes and run a query that fetches all nodes:

MATCH (n) RETURN n

Now change to Coordinate layout in the selector on the lower right part of the screen (and unless it’s already the case, you need to set location as the property to use for the coordinate). Zoom out so you see the entire graph and pull the sliders for X and Y, and you’ll start to see familiar shapes from all the airports.

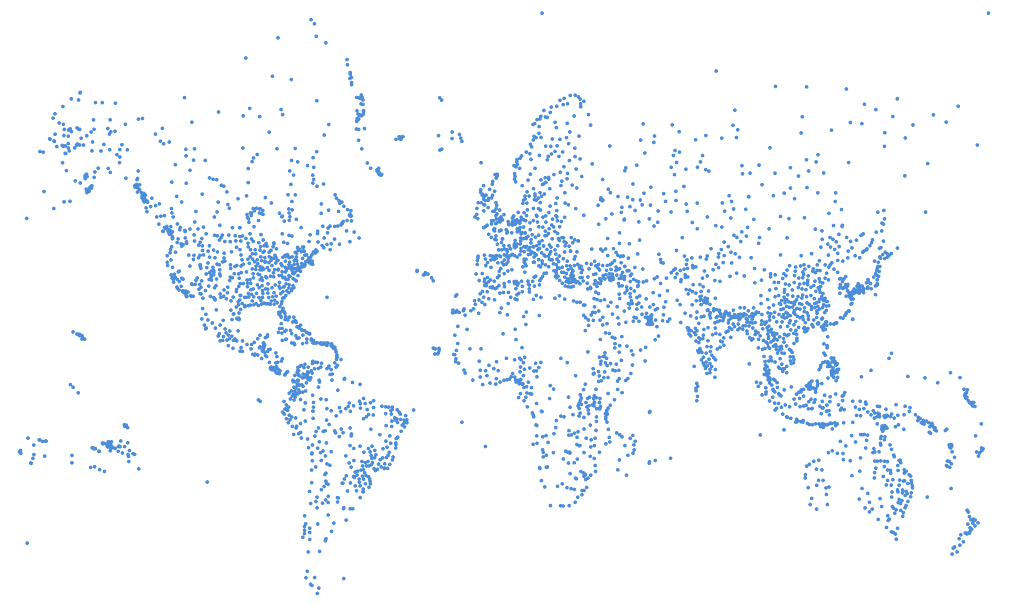
Now we can click Command+A or Ctrl+A to select all nodes, then we can click the right mouse button while over a node and select Expand > All in the popup menu, and we’ll see all routes as well.

That’s it. Now we have the data needed for our use cases for REPEATABLE ELEMENTS.

Use Cases

Here are a couple of different use cases for REPEATABLE ELEMENTS, all using the airport data from above.

The Isolation of Ísafjörður

I live in Malmö, Sweden, where we have an airport called Malmö Airport, nicknamed “Sturup” (IATA code MMX). We rarely fly from this airport because it’s quicker and easier to get to Copenhagen Airport, Denmark, which is also a lot bigger. But for the sake of this use case, we’ll say I want to fly from Malmö Airport (maybe the bridge to Copenhagen is closed due to heavy winds).

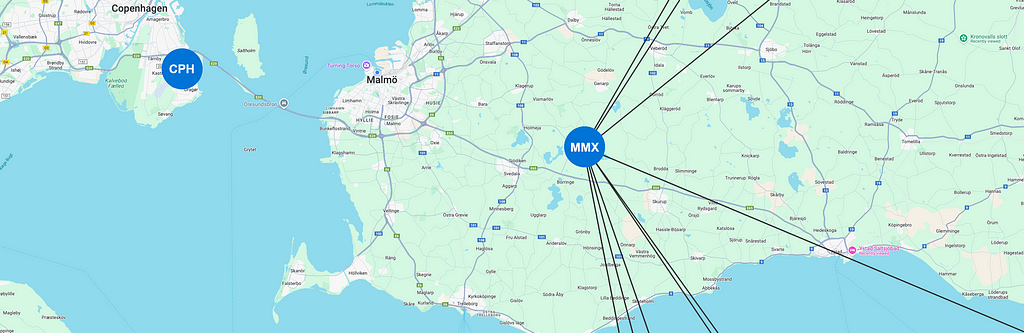
Now I get a sudden urge to fly somewhere right now (bad timing on this day when the bridge is closed). I don’t just want to fly somewhere and back but I want to take at least three flights. But there’s a limit to how much time I want to spend in security lines, so no more than five flights. How many possibilities do we have for this if we start in Malmö? Let’s see:

MATCH (mmx:Airport {iata: "MMX"})
MATCH p=(mmx)(()-[:CONNECTION]-()){3,5}(mmx)
RETURN p

This gives us 181,630 different travel options to choose from, and it would allow us to reach 6.4 percent (242) of the world’s airports, from Chicago in the west, Tromsø in the north, Tokyo in the east, and Addis Ababa in the south.

I have a friend who lives in Ísafjörður in north-western Iceland (no, actually I don’t, but let’s pretend I do), and he heard about my amazing experiences in Tromsø and wants to do the same thing. So let’s just update our query for Ísafjörður (IATA code IFJ):

MATCH (ifj:Airport {iata: "IFJ"})
MATCH p=(ifj)(()-[:CONNECTION]-()){3,5}(ifj)
RETURN p

It yields zero results! Why is that? Icelandair does operate flights to and from this airport. The reason is that there is just one connection, to Reykjavik, and since we have to use that on the outbound flight, we cannot use it for coming back again (remember, we cannot traverse the same relationship twice).

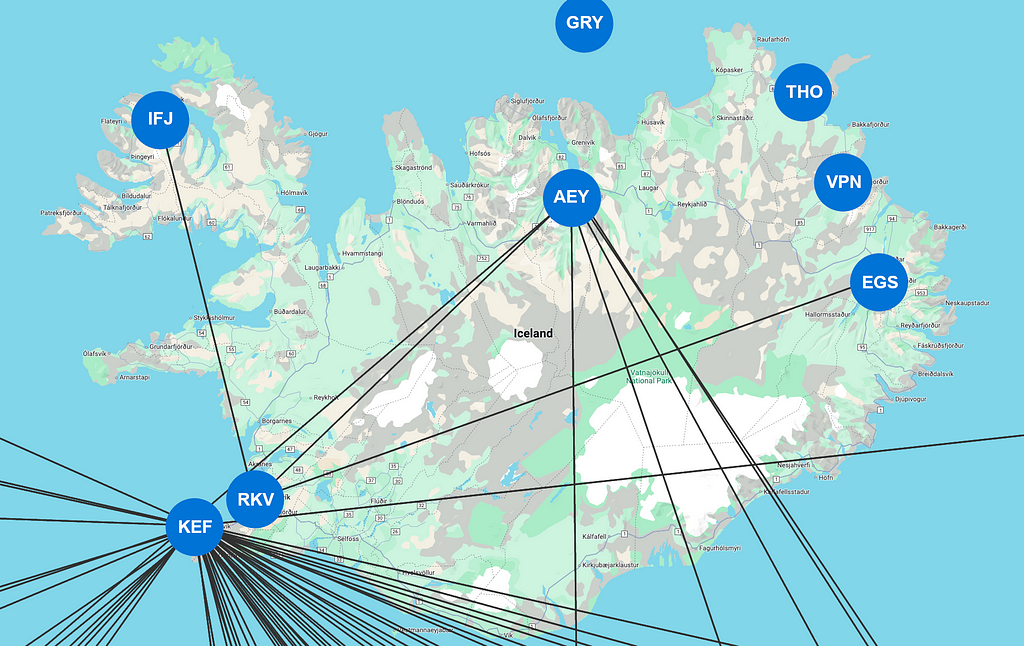
The solution is to use the new REPEATABLE ELEMENTS to allow the connections to be revisited:

MATCH (ifj:Airport {iata: "IFJ"})
MATCH REPEATABLE ELEMENTS p=(ifj)(()-[:CONNECTION]-()){3,5}(ifj)
RETURN p

Now we get a result. Unfortunately for my friend, we only get three matches, and he doesn’t get to leave Iceland. The reason is that Reykjavik is a domestic airport with just two other routes (the international airport is Keflavík, 30 miles outside Reykjavik). So in four steps, we get to either Akureyri or Egilsstadir and back (or just to Reykjavik and back two times), and if we used the fifth hop, we wouldn’t get back to Ísafjörður. But at least REPEATABLE ELEMENTS lets us solve our query (even if it doesn’t solve the isolation of Ísafjörður).

I Would Fly 500 Miles

We’ll look at another use case using our airport graph, this time in the spirit of The Proclaimers’ “I’m Gonna Be (500 Miles).” Walking 500 miles sounds terribly exhausting, so we’ll fly it instead.

Do we have any mileage chasers out there? Imagine we’re 500 miles short of keeping our airline status, which we absolutely don’t want to lose. So let’s take a tour, like in the previous section, with the goal of earning those 500 status points. Since there’s some correlation (in reality, rather weak, but we’ll assume there is) between the distance and the price of the ticket, and since we’re frugal, we want to keep the distance as low as possible, while still being above 500.

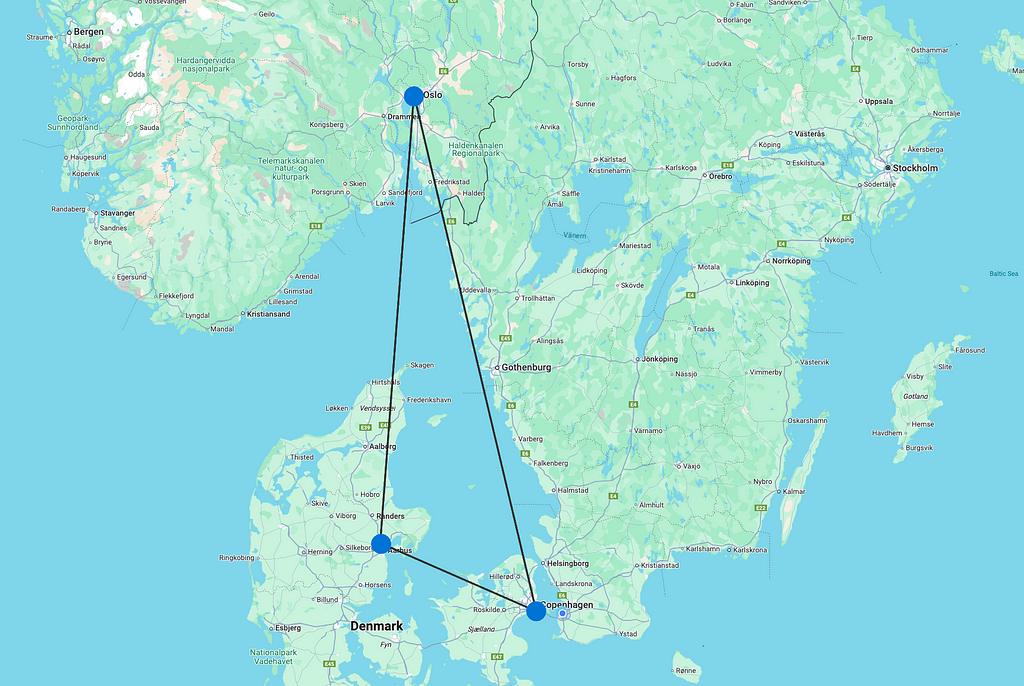
This time, I only want to fly with Scandinavian Airlines for my flight status (we’ll ignore airline alliances for now). The three main hubs for this airline are Copenhagen, Stockholm, and Oslo. So for this, I certainly hope the winds have settled on the bridge so we can get over to Copenhagen instead of Malmö.

The distance we have on the connections are in kilometers (km), and 500 miles is equal to 805 km. Our query will be to depart from Copenhagen and make two to six jumps and end up in Copenhagen again, with the goal of being as close to 805 km as possible (while still being above). The reason for setting the limit to six is that few flights are shorter than 150 km.

MATCH (cph:Airport {iata: "CPH"})
MATCH p=(cph)(()-[c:CONNECTION]-() WHERE "Scandinavian Airlines" IN c.carriers){2,6}(cph)
WITH p, reduce(d = 0, c IN relationships(p) | d + c.km) AS distance
WHERE distance >= 805
ORDER BY distance LIMIT 1
RETURN p, distance

The proposal we get is to fly from Copenhagen to Oslo (516 km), from Oslo to Aarhus (433 km), and back to Copenhagen (147 km), which adds up to 1,096 km (681 miles).

That’s overshooting by quite a bit; do they think I’m made of money? We need to find a more optimal variant. Again, REPEATABLE ELEMENTS to the rescue. We know that just going to Oslo and back would be shorter, while still more than 500 miles, so allowing the reuse of connections will certainly help. Here’s a query with REPEATABLE ELEMENTS (I also added a filter to only consider flights shorter than 548 km, since we already have a solution that is twice that):

MATCH (cph:Airport {iata: "CPH"})
MATCH REPEATABLE ELEMENTS p=(cph)(()-[c:CONNECTION]-() WHERE c.km < 548 AND "Scandinavian Airlines" IN c.carriers){2,6}(cph)
WITH p, reduce(d = 0, c IN relationships(p) | d + c.km) AS distance
WHERE distance >= 805
ORDER BY distance LIMIT 1
RETURN p, distance

When allowed to fly between the same airports more than once, we get a shorter option: a round trip to Torp, which is an airport by the Norwegian coast just south of Oslo, 420 km from Copenhagen. So the total trip ended on 840 km (522 miles). And with that, we have our flight status secured for another year.

I am glad Torp was there since the second-best alternative would have been to fly to Aarhus and back three times, and that would have been a bit too monotonous.

Visiting an Imaginary Friend

Cypher has a keyword called SHORTEST that allows you to find the shortest path (in number of hops, not the weight of the hops) in the graph. This now supports REPEATABLE ELEMENTS.

Wait a minute — you may say, for shortest path, there can certainly never be a need to repeat a relationship! Well, no, not if you want the absolute shortest path between two points. But if you have a lower hop limit or if you have some other special rules for your path, there may be. Let’s look at another example.

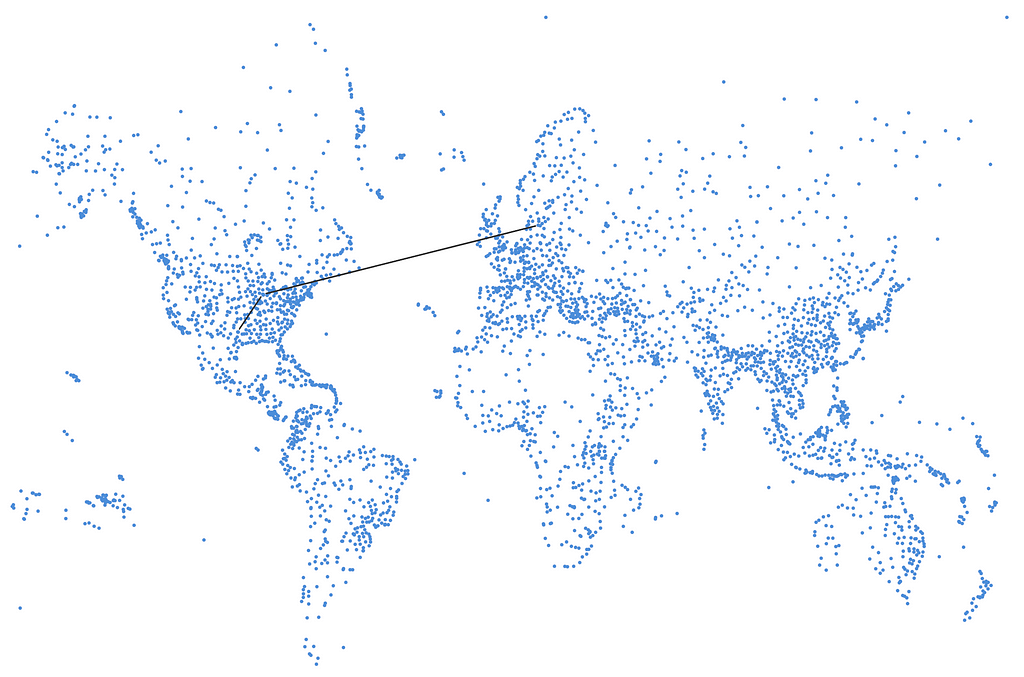
I want to fly from Copenhagen to Dallas to visit some friends (this time, actual, real-life friends) and I want to do it in as few flights as possible. We can do that like this:

MATCH p = ALL SHORTEST (:Airport {iata:"CPH"})--+(:Airport {iata:"DFW"})
WITH p, reduce(d = 0, c IN relationships(p) | d + c.km) AS distance
ORDER BY distance LIMIT 1
RETURN p

The first statement is the one that finds the shortest path (in the fewest flights). We have ALL SHORTEST (instead of SHORTEST 1), which returns all the shortest paths instead of just one. Then we order them by the total distance and select the shortest (by distance). There could still be flights that have a shorter total distance, with more hops, but we aim at having fewer flight changes, and that gives us an option with one change in Chicago.

Let’s add another condition here. Remember my imaginary friend in Ísafjörður? I know that because of Earth’s curvature, flights from Northern Europe to North America usually fly over Iceland, so why not make a stop to visit him as well? That would be a query like this:

MATCH p = ALL SHORTEST (:Airport {iata:"CPH"})--+(:Airport {iata:"IFJ"})--+(:Airport {iata: "DFW"})
WITH p, reduce(d = 0, c IN relationships(p) | d + c.km) AS distance
ORDER BY distance LIMIT 1
RETURN p

But we don’t get any results, and we already know why: To get to Ísafjörður, we need to use a route that we’ll reuse when continuing our trip. So again, we need to turn to REPEATABLE ELEMENTS to solve it:

MATCH REPEATABLE ELEMENTS p = ALL SHORTEST (:Airport {iata:"CPH"})--{,10}(:Airport {iata:"IFJ"})--{,10}(:Airport {iata: "DFW"})
WITH p, reduce(d = 0, c IN relationships(p) | d + c.km) AS distance
ORDER BY distance LIMIT 1
RETURN p;

Notice that the + is replaced with {,10}. This is because we aren’t allowed to have infinite quantifiers when using REPEATABLE ELEMENTS. Just think about it a bit.

And with this, we get a nine-hop route through Keflavík (the international airport of Reykjavik), but we have to fly to Akureyri to get over to the domestic airport of Reykjavik, then up to Ísafjörður. Then we need to traverse the same way back to Keflavík, and from there, we continue to Dallas through Chicago.

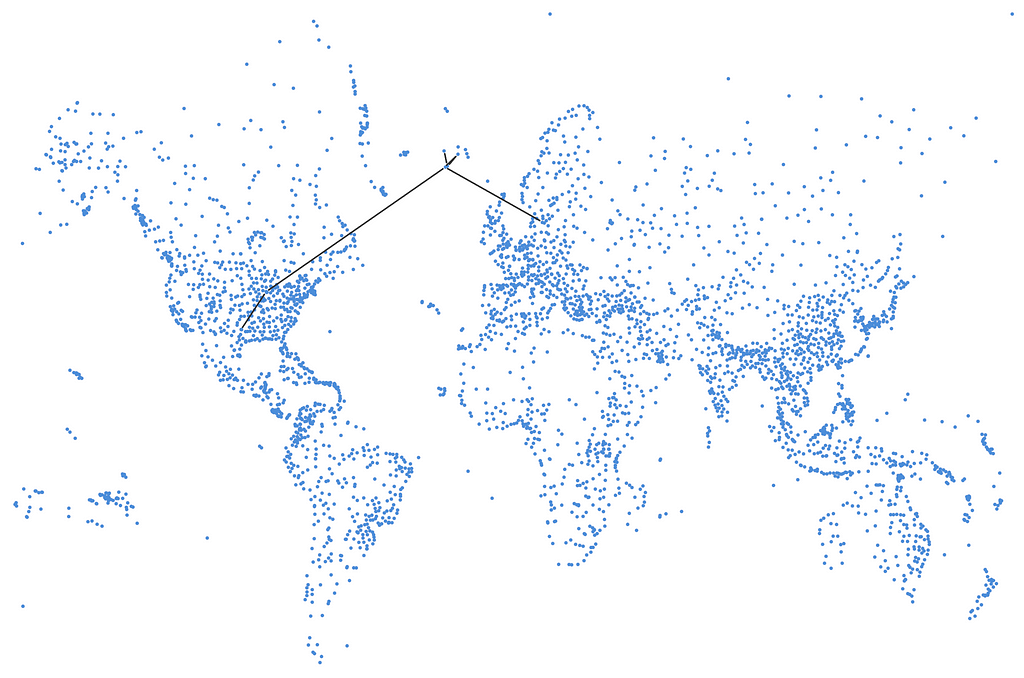
A conclusion from looking at this is that it would probably have been better to take a taxi the 50 km between Keflavík and Reykjavik. That would have saved us four flights (out of nine) and a total of 1,066 km in the air. But you don’t get free peanuts in the taxi.

Summary

By the examples we looked at here, I realize that it seems like REPEATABLE ELEMENTS is only beneficial when we want to traverse the same relationship in both directions. But it can also be that we want to revisit relationships in the same directions. If we turn back to the first example graph in this article and say we want the shortest path from a to e, but with at least six jumps, we won’t get a result unless we use REPEATABLE ELEMENTS:

MATCH REPEATABLE ELEMENTS p = SHORTEST 1 (a {name: "a"})-->{6,10}(b {name: "e"})
RETURN p

This gives us a result with two loops through c and d.

For most traditional uses of Neo4j and Cypher, the default match mode with DIFFERENT RELATIONSHIPS is probably what you want. But as we’ve seen, there are certainly cases where it’s beneficial to be able to traverse the relationships multiple times.

You can read more about match modes and REPEATABLE ELEMENTS in the Cypher documentation. If you have questions, you can post in the Neo4j Community Forum.

---

I Would Walk 500 Miles was originally published in Neo4j Developer Blog on Medium, where people are continuing the conversation by highlighting and responding to this story.