Common Graph Structures - Graph Data Modeling for Neo4j

About this module

At the end of this module, you will be able to:

Describe common graph structures used in modeling:
- Intermediate nodes
- Linked lists
- Timeline trees
- Multiple structures in a single graph

Intermediate nodes

You sometimes find cases where you need to connect more data to a relationship than can be fully captured in the properties. In other words, you want a relationship that connects more than two nodes. Mathematics allows this, with the concept of a hyperedge. This is impossible in Neo4j.

You create intermediate nodes when you need to:

Connect more than two nodes in a single context.
- Hyperedges (n-ary relationships)
Relate something to a relationship.

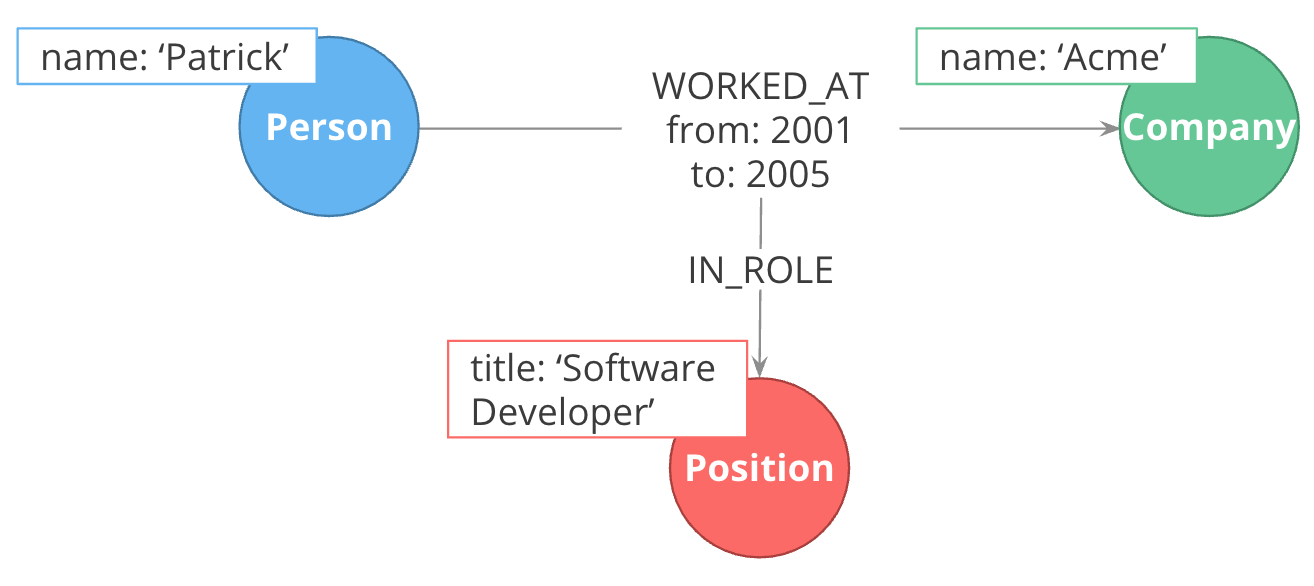
Here we have the WORKED_AT hyperedge that has the from and to properties, but we need to associate the role with this period of work. In Neo4j, there is no way to create a relationship that connects a relationship to a node. Neo4j relationships can only connect nodes.

Using intermediate nodes

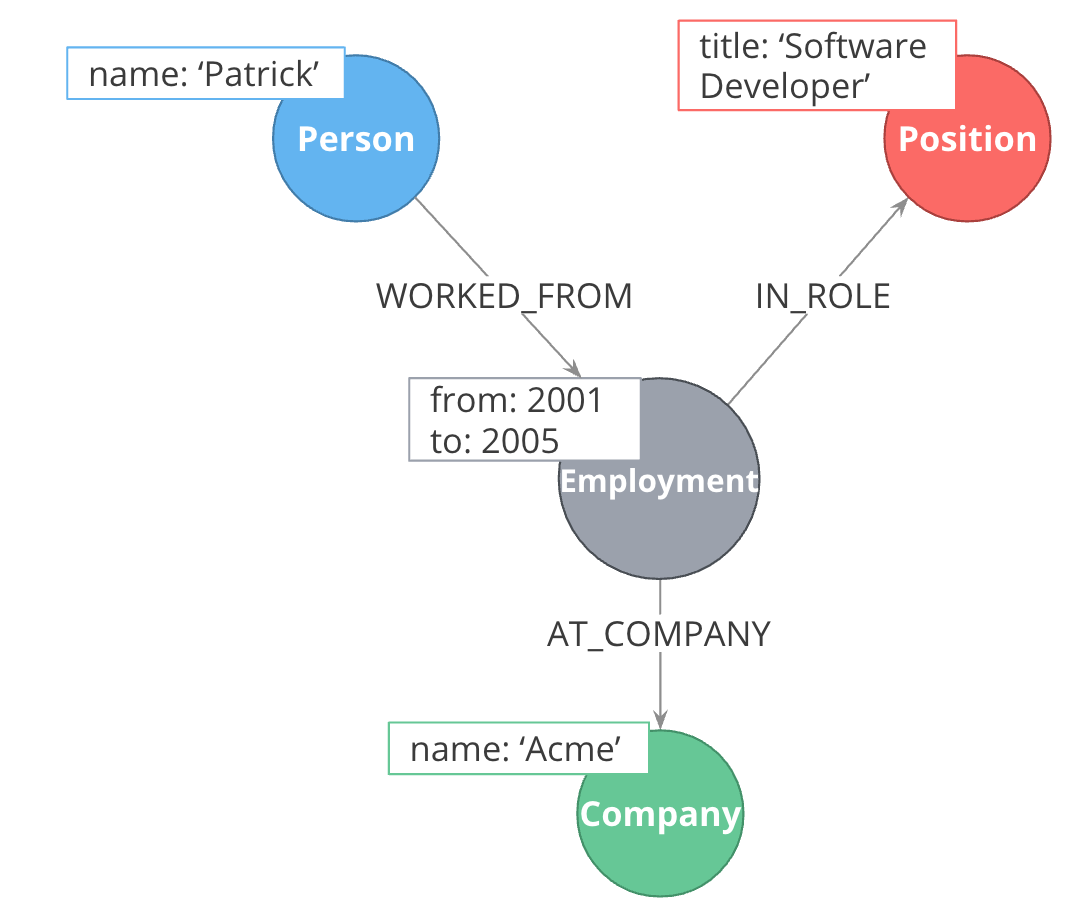
The solution is to replace the hyperedge with a connection point node. Since nodes are connection points, you simply create a node in the middle of the hyperedge.

In this example, we replace the WORKED_AT hyperedge with an Employment intermediate node. This provides a connection point that allows us connect any amount of information to Patrick’s term of employment at Acme.

Intermediate nodes: sharing context

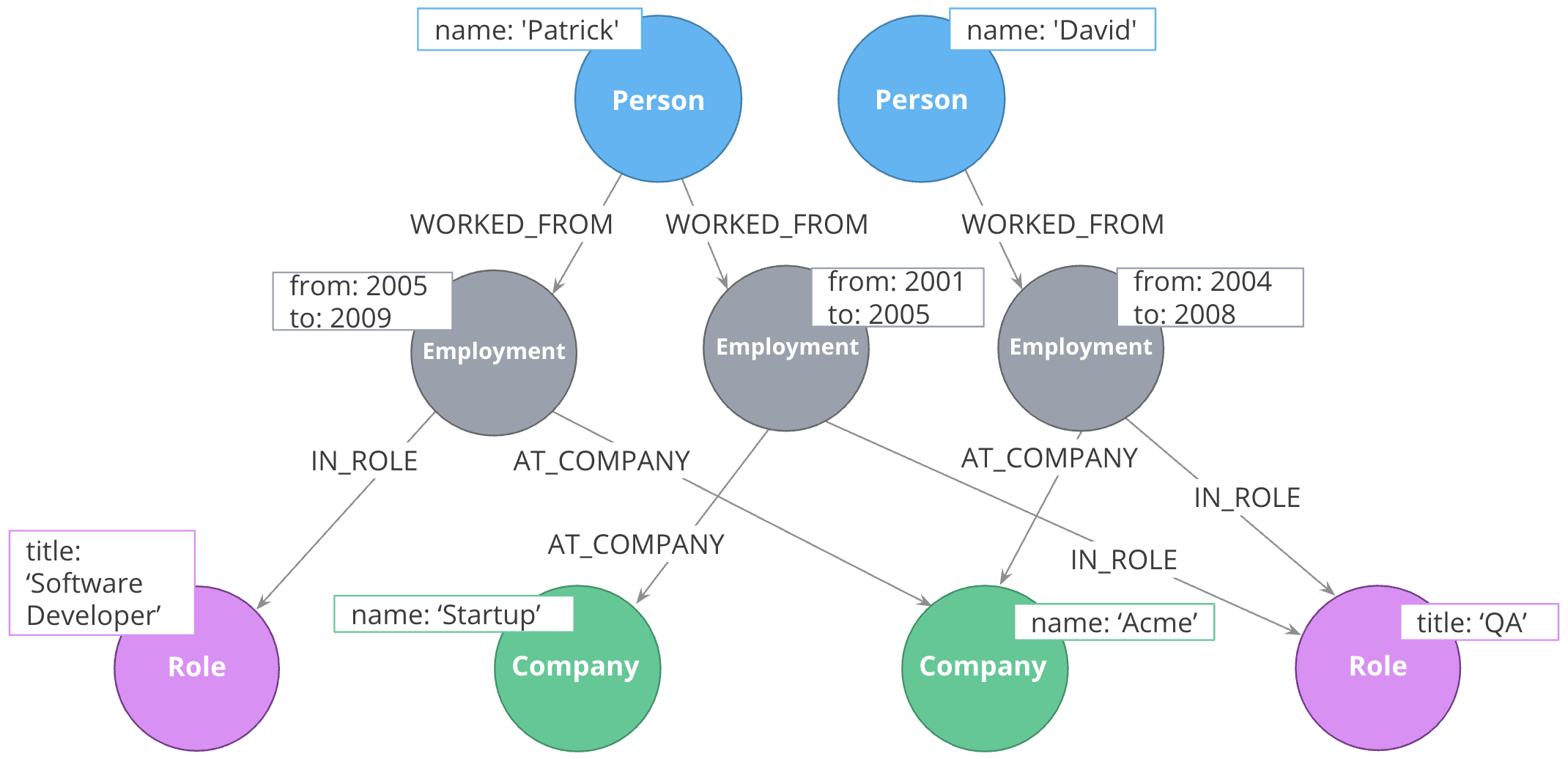
This model allows different employment events to share contextual information. Person nodes can have a shared Role or Company, and allow us to very easily trace either the full details of a single person’s career, or the overlap between different individuals.

Intermediate nodes: sharing data

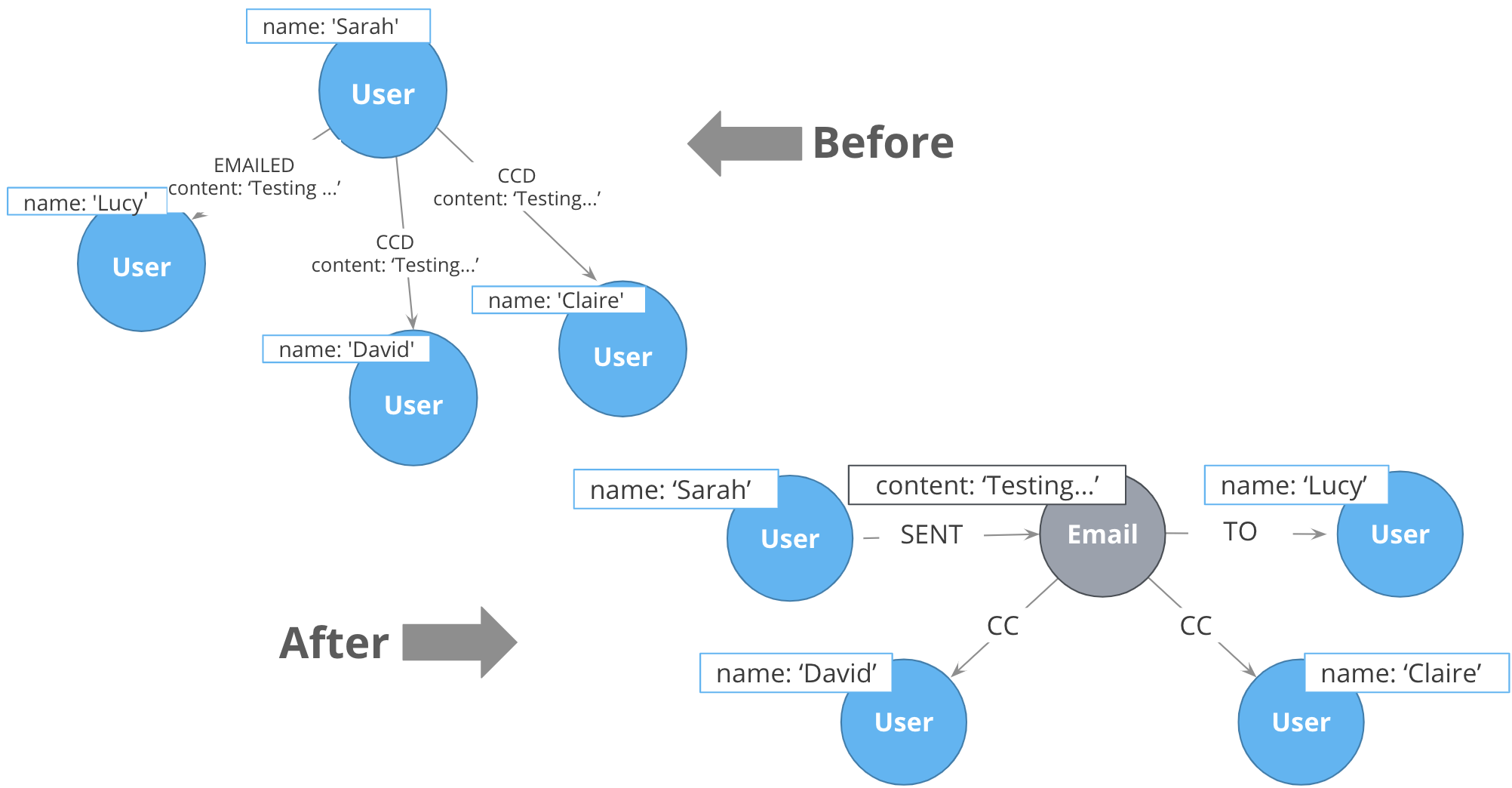
Intermediate nodes also allow you to deduplicate information. We mentioned a similar principle when we discussed fanout where splitting a property onto its own node allows you to reference it via a relationship instead of a repeated property.

In this case, the Email intermediate node spares us having to repeat the email content on every single relationship.

Intermediate nodes: organizing data

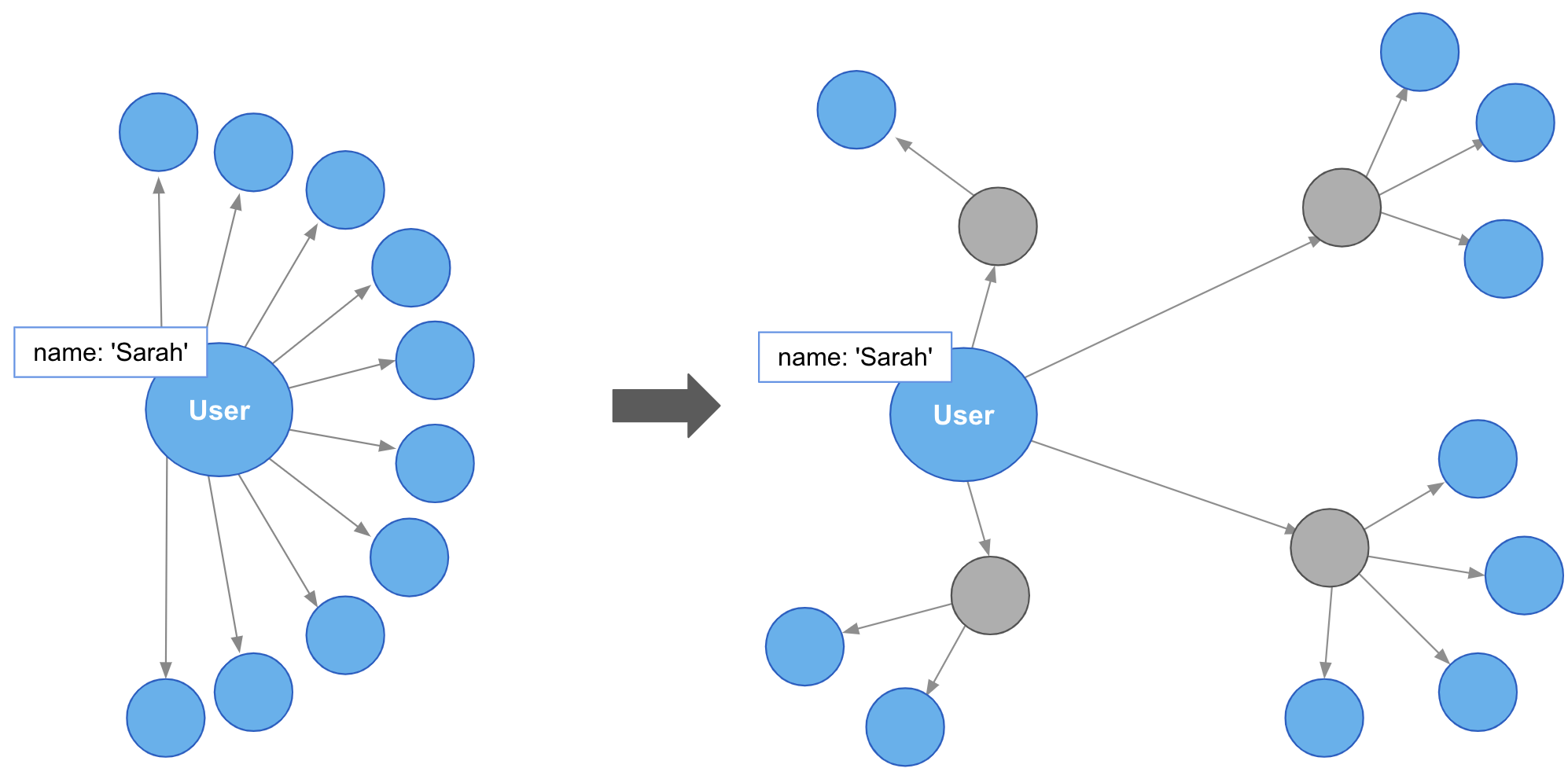
In addition, intermediate nodes can be invaluable organizing structures. This is a more expansive zoomed-out view of the same data as the previous example. The grey nodes are the Email intermediate nodes.

When we model Email as a relationship, as on the left, we encounter two problems. First, Sarah’s node becomes extremely dense. For every single recipient of any message she writes, she gains another relationship. On the right, she only has one relationship per email, regardless of the number of recipients. Dense nodes can be tricky to work with.

Second, it is difficult and expensive to determine who in Sarah’s recipient network has received a given message. In the left model, we need to traverse every relationship and check the email content to see which messages are shared. This specific case requires between six and nine “wasted” hops, depending on whether we are looking for the four-recipient message or the one-recipient message. On the right, with the Email intermediate node, we still need to check every message. But having done so, we can guarantee that every node connected to that email is a relevant one. There will only ever be three “wasted” hops.

Linked lists

Linked lists are useful whenever the sequence of objects matters. The typical pattern is to define relationships between sequential items with the names NEXT or PREVIOUS, although those words are not verbs. As always, choose one or the other based on the questions you expect to ask.

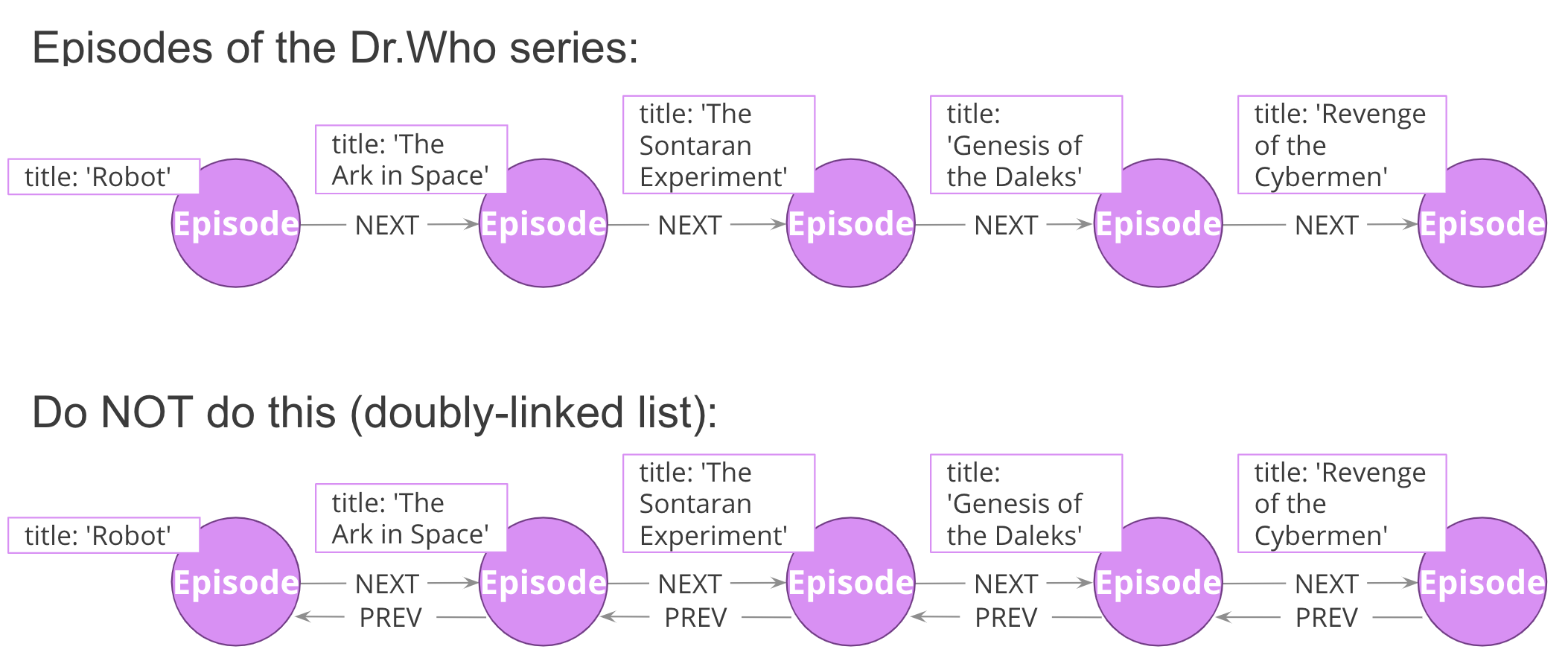
Linked lists are not unique to graphs. They are a common pattern in lots of data modeling paradigms. In some of those paradigms, you see both the singly-linked list (above) and the doubly-linked list (below).

However, singly-linked lists in Computer Science are one-way: they have a destination but no sure information. Neo4j relationships tracks both from and to node, so they are different from Computer Science singly-linked lists.

The power of a Graph Database is that the To-From relationship is maintained in the database, whereas in a Traditional Relational Database a row with a Primary Key has no information about who is pointing to it.

Never use a doubly-linked list in Neo4j because doubly-linked lists use redundant symmetrical relationships.

Interleaved linked list

You can add complexity to linked lists. Sometimes, there are multiple ways you could sequence a set of items.

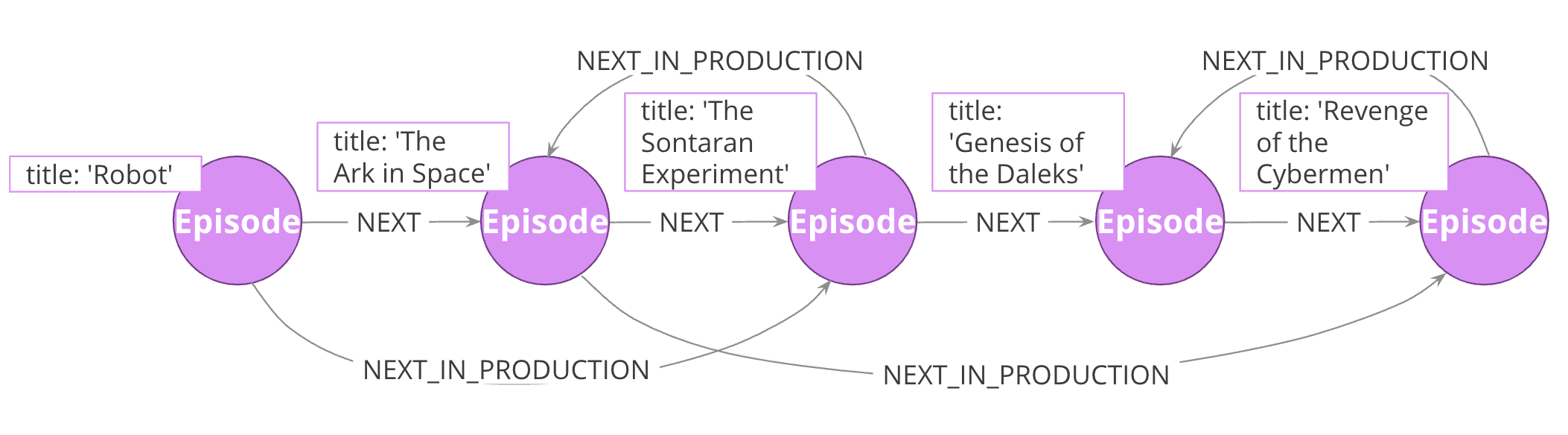
For example, the order in which TV show episodes are shown is not always the same order in which they were created. Here, we again have the episodes of Dr. Who season 12, but with two sequences: the order of airing (NEXT) and the order of production (NEXT_IN_PRODUCTION).

Head and tail of linked list

Here is another pattern that uses a linked list. When working with linked list, there is generally a “parent” node that is used as the entry point. That parent almost always points to the first item in the sequence, using an appropriately named relationship. It may also point to the last item. For cases where you are tracking progress through the sequence, the parent node may also have a pointer to the “current” item.

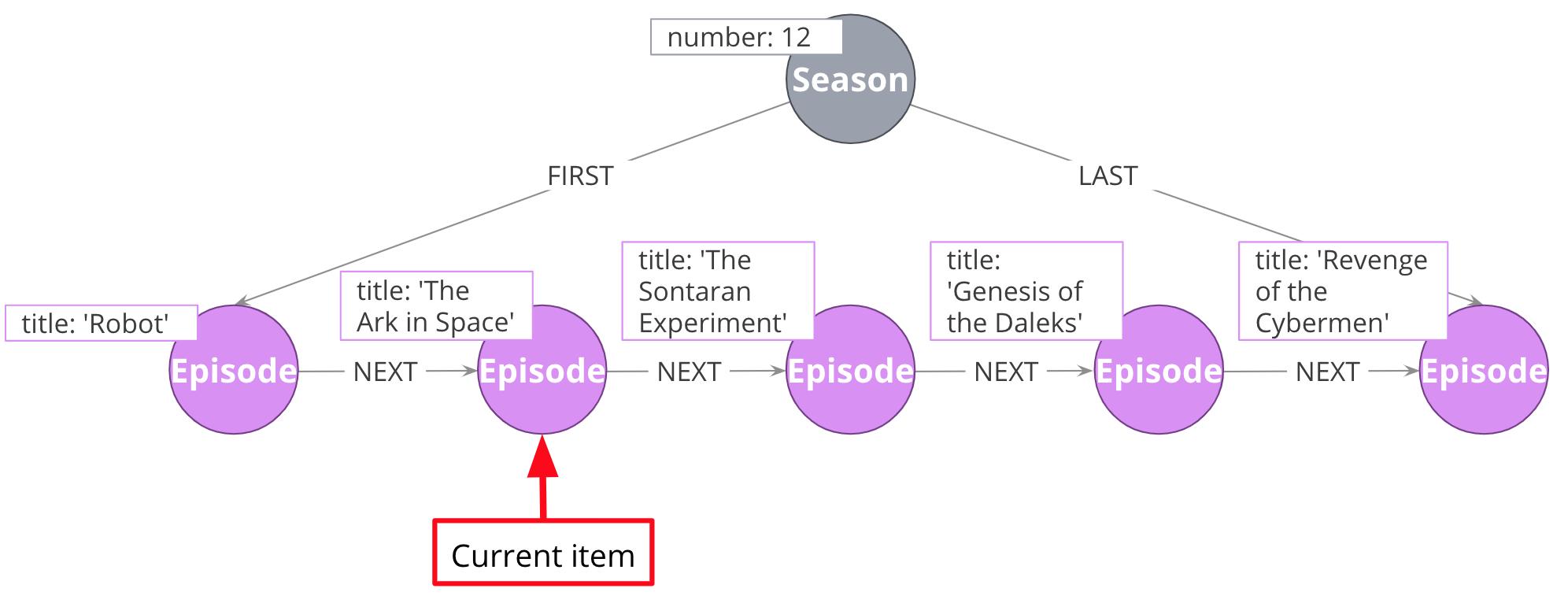
Some possible use cases:

Add episodes as they are broadcast.
Maintain pointer to first and last episodes.
Find all episodes broadcast so far.
Find latest episode broadcast so far.

Timeline tree

Trees are not complicated, but you will learn about one special kind of tree, the timeline tree. Timeline trees can be a useful structure when you want to use time as either an anchor or a navigational aid in your querying, and when the periods of time that interest you vary.

The topmost node in the timeline is an “all time” node. That then subdivides into whatever time periods interest you.

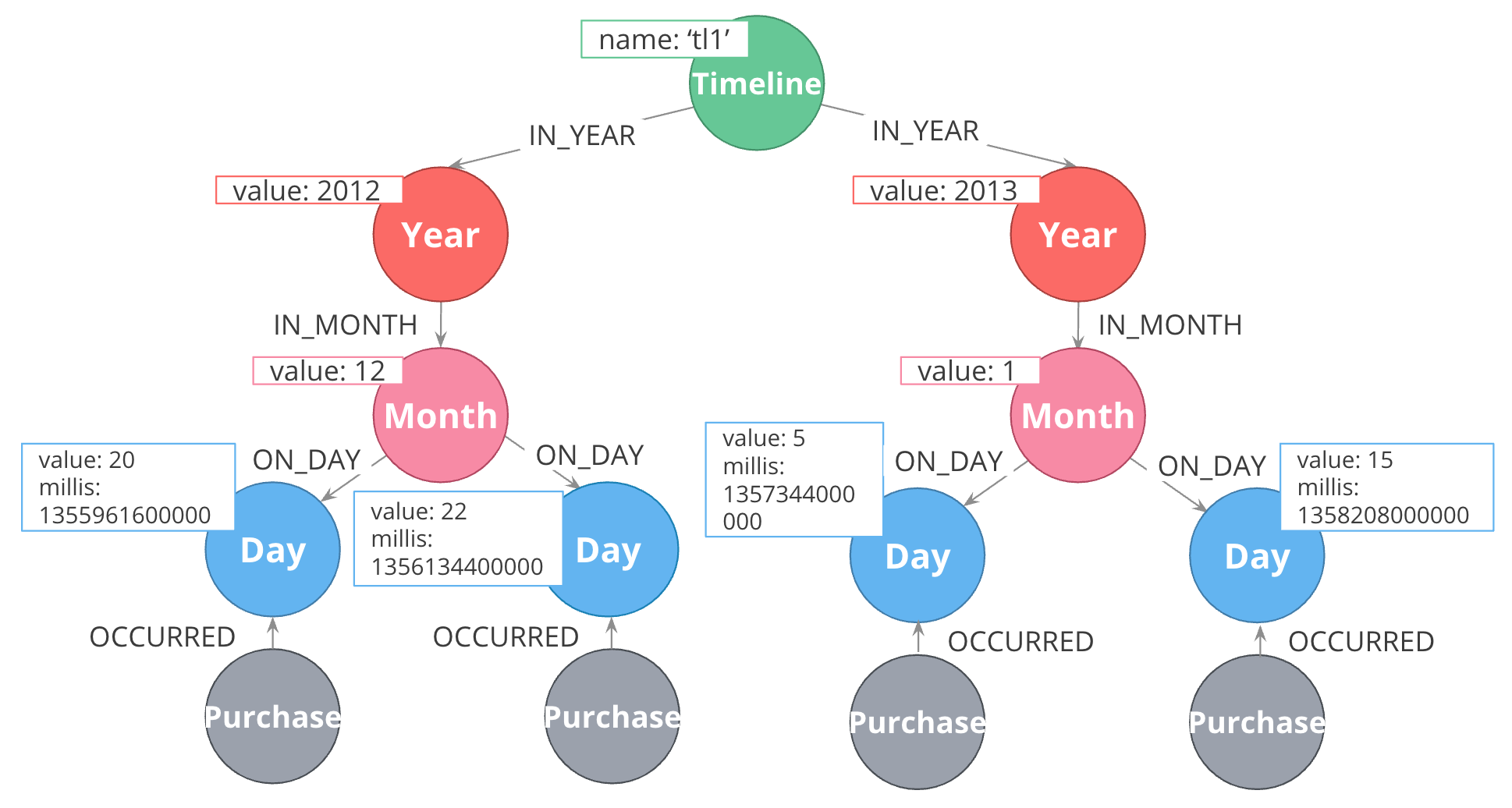
Here, we have chosen years, months, and days; we could just have equally chosen quarters, weeks, hours, minutes, or anything else. All of our “data” nodes then link into the timeline tree at the appropriate leaf node. Here, we have connected every purchase to a day.

With this structure, some otherwise-expensive time questions become easy. For example, finding all purchases in a given time period, where the period of interest might be a day, a month, or a year, depending on circumstances. Simply anchor on the timeline at the appropriate time period of interest, then traverse downward through the tree.

What is more interesting, though, is dealing with time when time is part of the traversal, but not the anchor. For example, looking for all purchases that happened within a some time period relative to another event. You anchor on the specified event, traverse into the timeline tree, traverse to the appropriate time period of interest, then traverse downward. Without a timeline structure in the graph, this kind of query frequently involves a lot of property lookups and inefficient gather-and-inspect.

That is not to say that timeline trees are the go-to “best” method of expressing time! Quite the opposite—timeline trees consume a lot of space relative to the data they contain. Most often, even when time is an important part of the answer to a question, a simple property is sufficient.

But we are sharing this structure with you so that, in cases where a property alone is not good enough, you do not need to reinvent the concept of a timeline tree yourself.

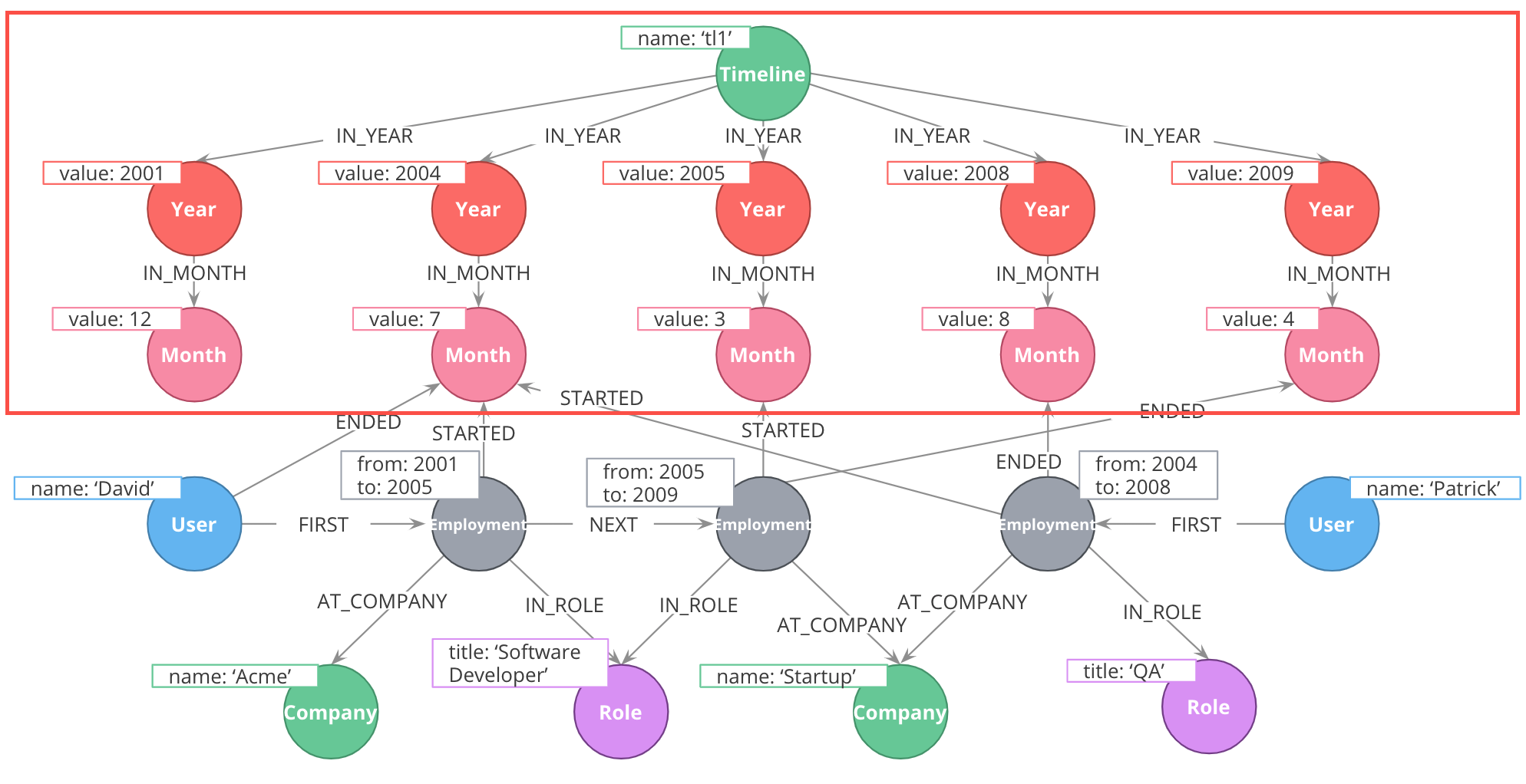
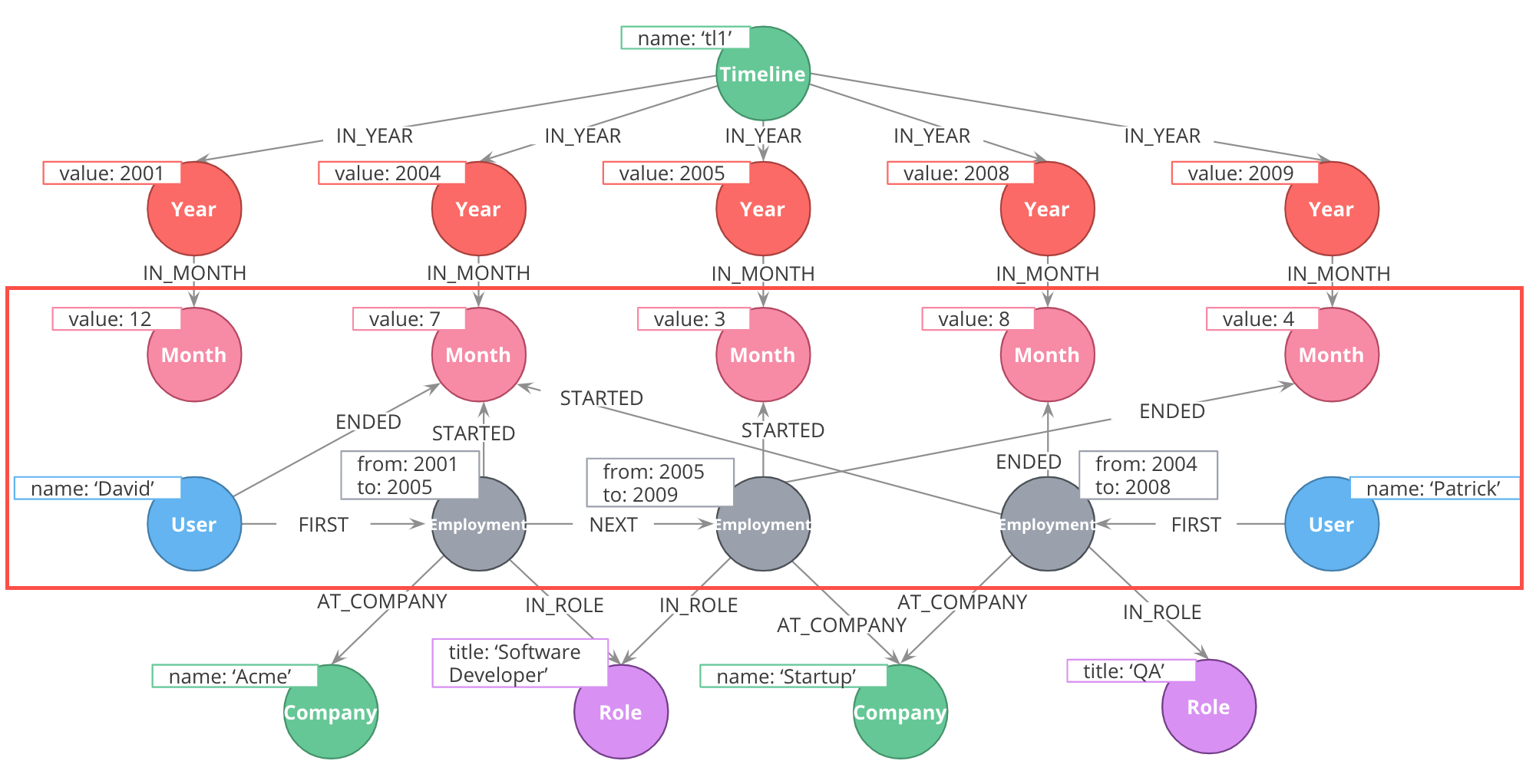
Using multiple structures

All of the structures you have learned about thus far are not entire models in their own right. They are tiny patterns with specific use cases. Modeling questions as a whole are usually larger and more complex than that. Frequently, you will see multiples of these structures used together in order to fully solve a problem.

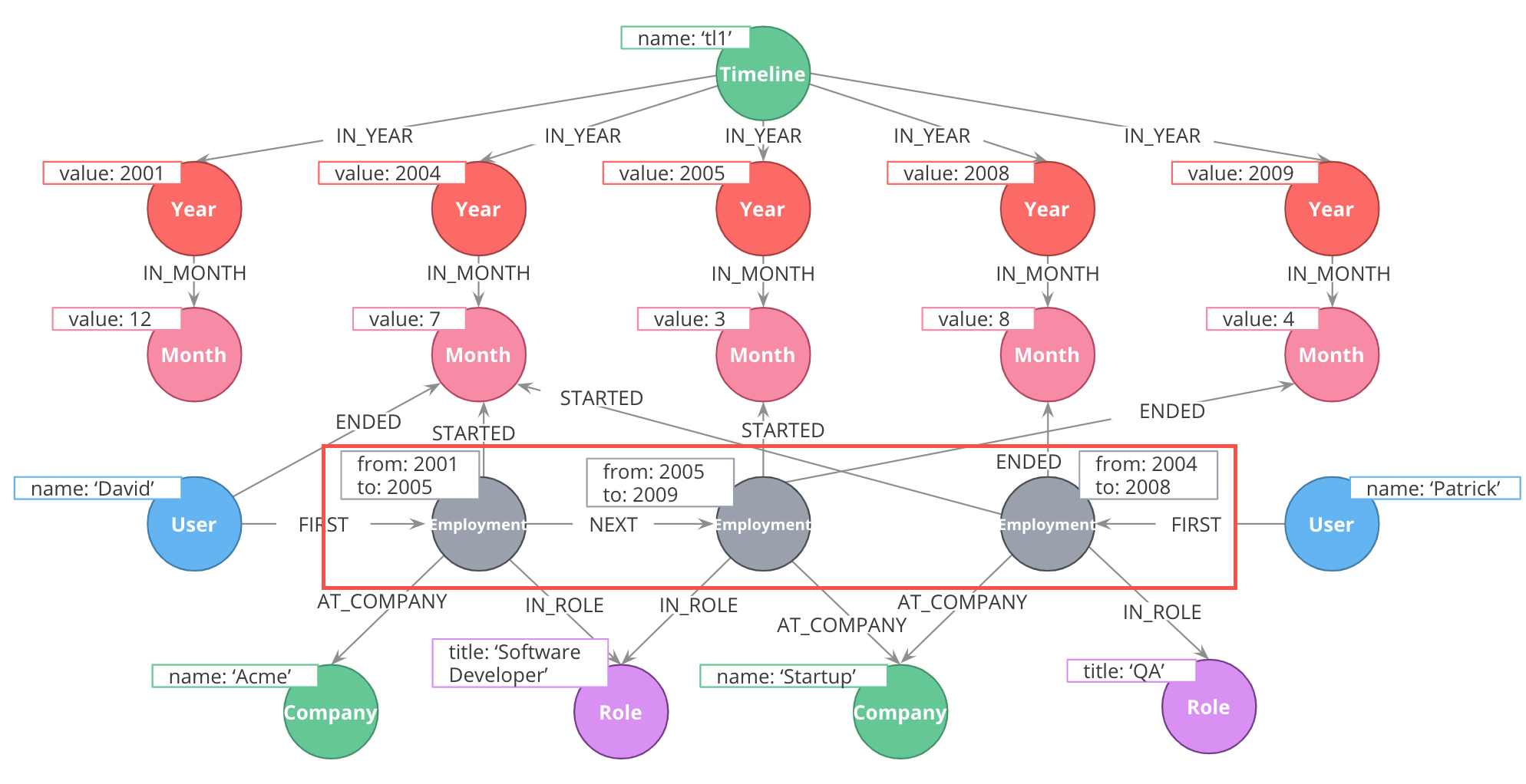
Here is one example.

Using the timeline tree

At the top, we have a timeline tree that subdivides into years and months.

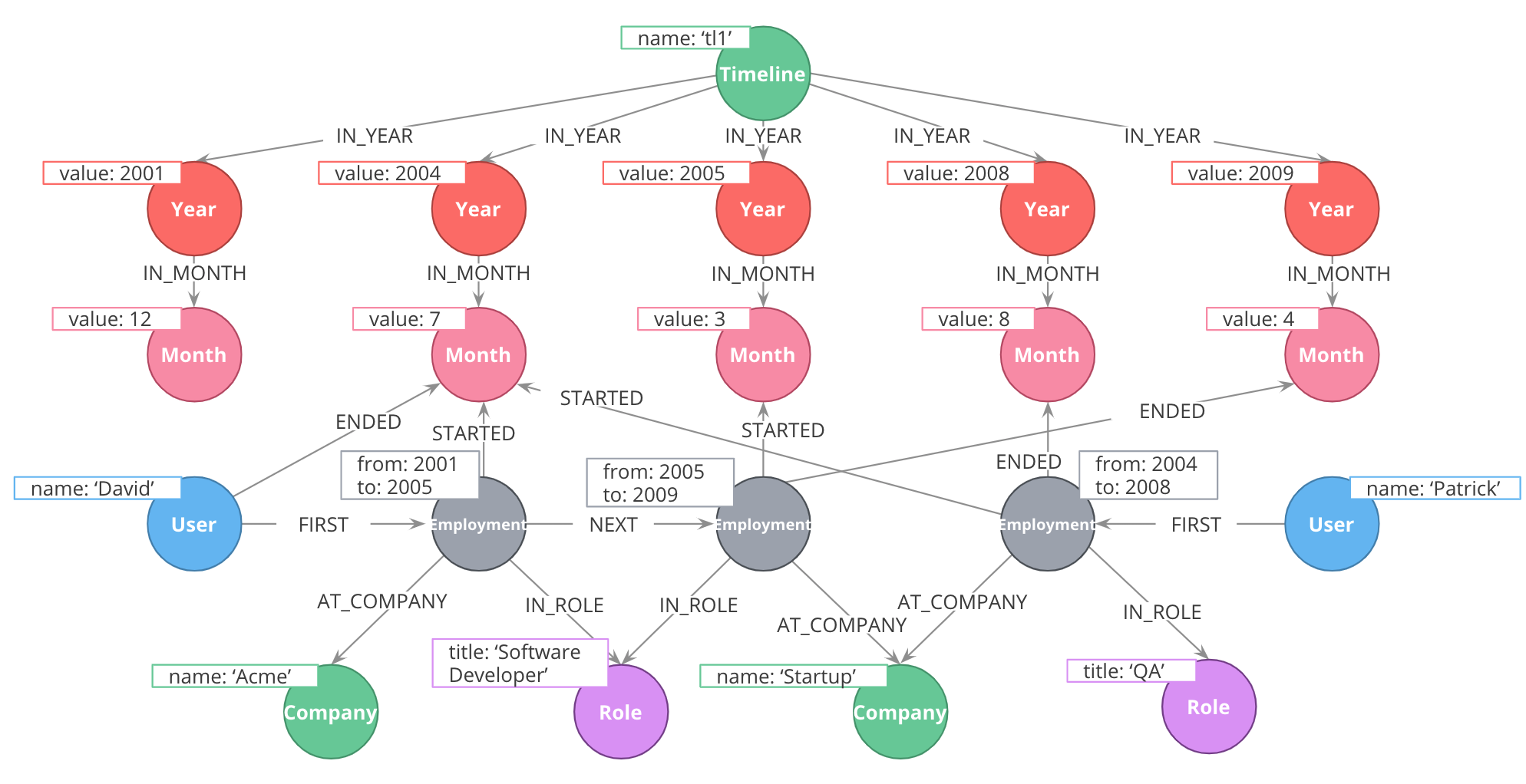
Using intermediate nodes

The relevant items connected to the timeline are Employment events, which link to the starting and ending months of that employment. Employment events themselves are intermediate nodes connecting people, companies, and job roles. In this case, the intermediate nodes are serving the dual purposes of reducing the density of Person nodes, and providing an attachment point for the timeline tree.

Using linked list

Furthermore, the Employment events themselves are organized into linked lists for each person. This allows us to represent the sequence of employment events in an individual’s career.

Exercise 4: Model a Learning Management System (LMS)

Given a description of the domain, sample data, and the application questions:

Create the model (entities and connections) using the Arrows tool.
- Look for any use cases that will use some common patterns you have learned about.
Add sample data to the model using the Arrows tool and confirm questions can be answered using the model.

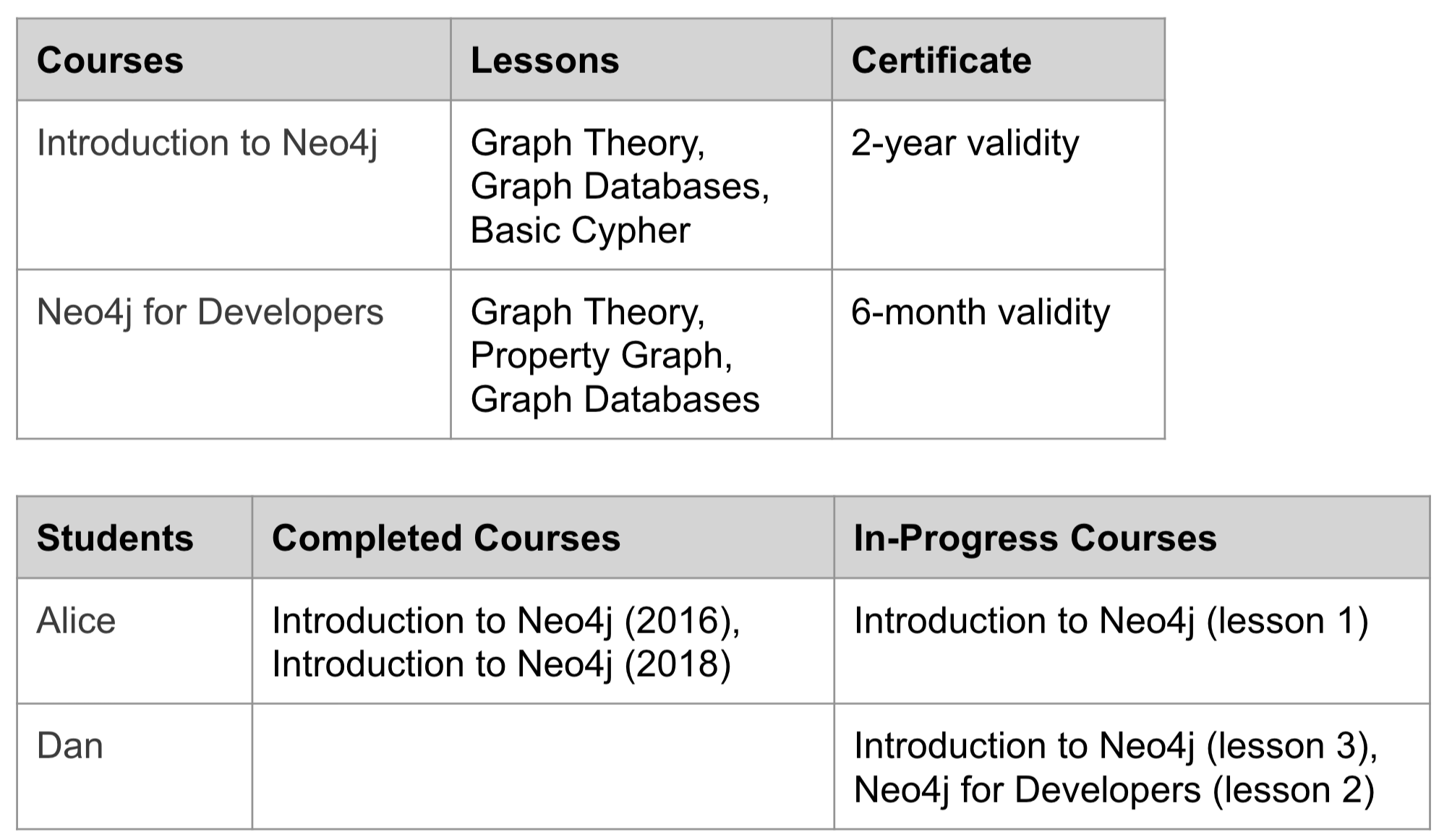
Exercise 4 instructions: The domain

There are many courses in the LMS, each of which contains a number of lessons that must be completed in a specific order.
Every course grants a certificate upon completion.
This certificate has a term of validity. When it expires, students must take the course again.
Students can enroll in as many simultaneous courses as they want to.
When a student logs in and chooses a course, the LMS must send them to their latest unfinished lesson.

Exercise 4 instructions: Sample data

Exercise 4 instructions: Application questions

Which lesson(s) is Dan currently working on?
What are Alice’s current certifications?
Which lessons are in the Neo4j for Developers course?
What is the last lesson in the Introduction to Neo4j course?
Which lesson follows Graph Theory in the Neo4j for Developers course?
Who has completed Introduction to Neo4j?

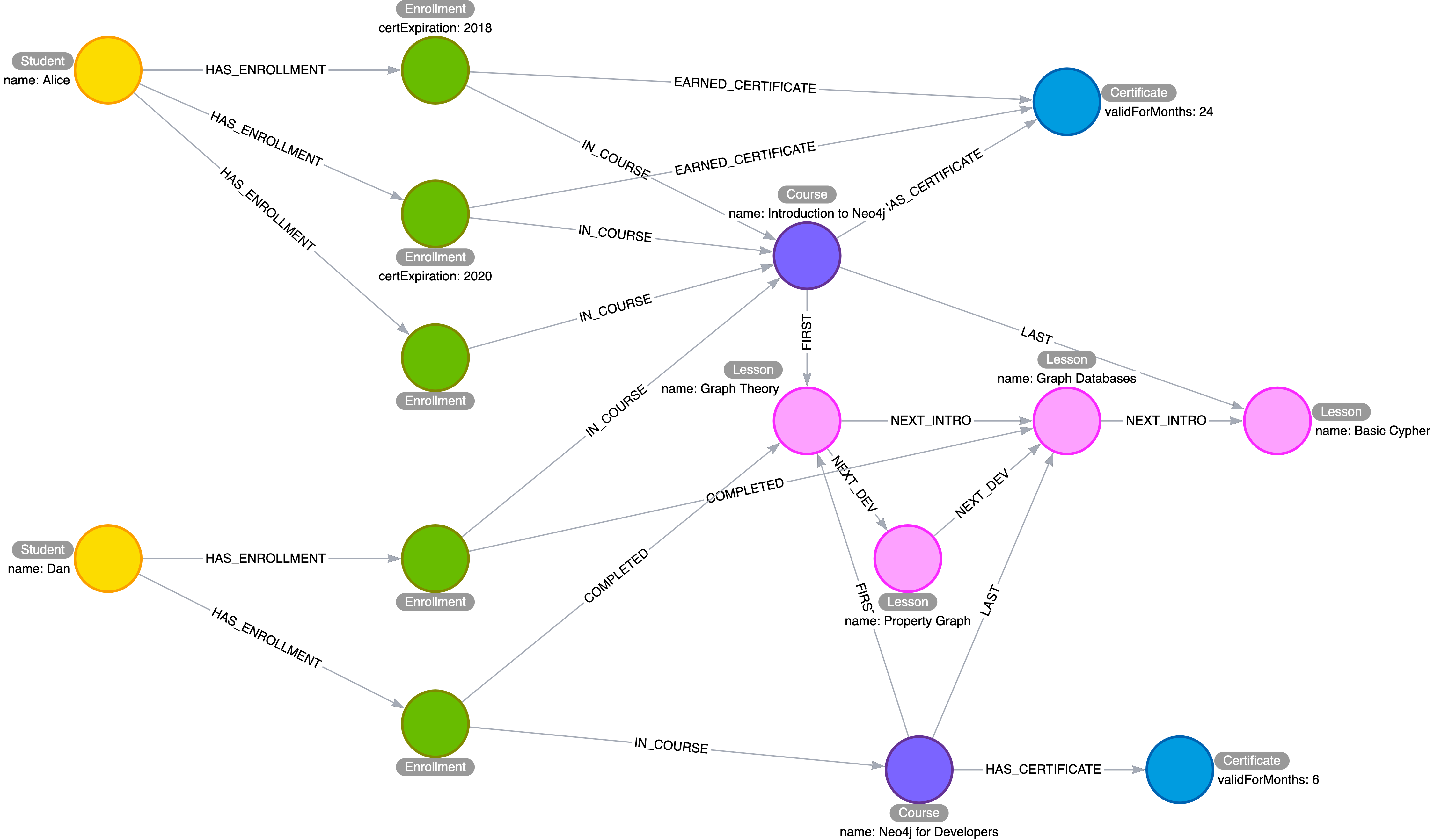
Exercise 4 solution: Application model

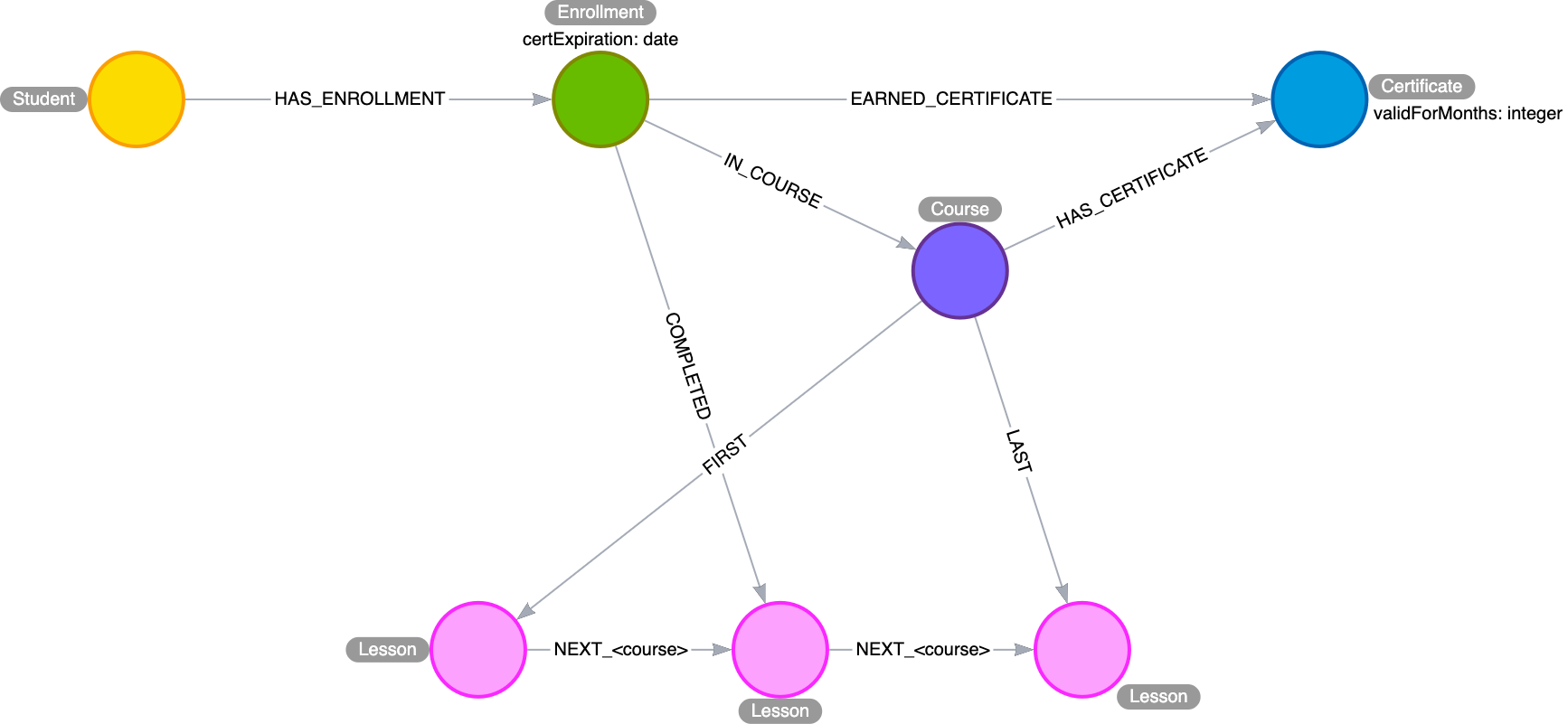
The Course and Lessons are structured as a linked list with a parent. We include the course name in the NEXT relationship, because some lessons are used by multiple courses, but in a different order. In other words, we have an interleaved linked list, and need to distinguish the different sequences.

Courses are associated with a Certificate, which contains, among other things, a term of validity expressed here in months.

Students do not directly interact with courses or lessons. Instead, we use an Enrollment intermediate node to organize their interactions. Enrollments are linked to a single course and contain a pointer to which lesson was most recently completed. When a COMPLETED relationship is created with the lesson marked LAST in a given course, that is the trigger to create an EARNED_CERTIFICATE relationship. At this point, the certExpiration property will be populated by adding the term of validity to the current timestamp. This intermediate node allows us to keep track of students’ progress through different concurrent courses, and to differentiate multiple subsequent passes through the same course.

Exercise 4 solution: Sample data

Check your understanding

Question 1

What graph modeling pattern can you use to add more contextual and organizational information to relationships that is not easily modeled with simple relationship properties?

Select the correct answer.

Sub-relationships.
Linked list.
Timeline tree.
Intermediate nodes.

Question 2

In Neo4j, which structure is not recommended as a best practice for representing linked lists?

Select the correct answer.

Interleaved linked lists with multiple starting points for navigation.
Doubly linked lists.
Single linked list.
Linked list with nodes that point to the head and tail of the list.

Question 3

What common structure is used to model data where you need to know when an event occurred in the application and find other events that occurred in the same time-frame?

Select the correct answer.

Linked list where each node has a timestamp.
Intermediate nodes where the intermediate nodes have time-related data.
Timeline tree
Doubly-linked list where the symmetric relationbship is the timestamp relationship.

Summary

You can now:

Describe common graph structures used in modeling:
- Intermediate nodes
- Linked lists
- Timeline trees
- Multiple structures in a single graph

Check Answers