Graph Data Science integration

Neo4j Graph Data Science algorithms can help you find new insights in your data, both into the nodes themselves as well as into how they are connected. See The Neo4j Graph Data Science Library Manual v2.2 for more information on graph algorithms.

Running Graph Data Science algorithms on elements in your Scene does not alter the underlying data. The scores only exist temporarily in Bloom.

The algorithms are described briefly below, but please refer to The Neo4j Graph Data Science Library Manual v2.2 for their full descriptions.

Available GDS algorithms in Bloom

The available algortihms can be divided into two categories, centrality and community detection. Centrality algorithms are used to measure the importance of particular nodes in a network and to discover the roles individual nodes play. A node’s importance can mean that it has a lot of connections or that it is transitively connected to other important nodes. It can also mean that another node can be reached in few hops or that it sits on the shortest path of multiple pairs of nodes. The following centrality algorithms are available in Bloom:

  • Betweenness Centrality

  • Degree Centrality

  • Eigenvector Cantrality

  • PageRank

Community detection algorithms on the other hand, are used to find sub-groups within the data and can give insight to whether networks are likely to break apart. Community detection is useful in a variety of graphs, from social media networks to machine learning. The following community detection algorithms are available in Bloom:

  • Louvain

  • Label propagation

  • Weakly connected components

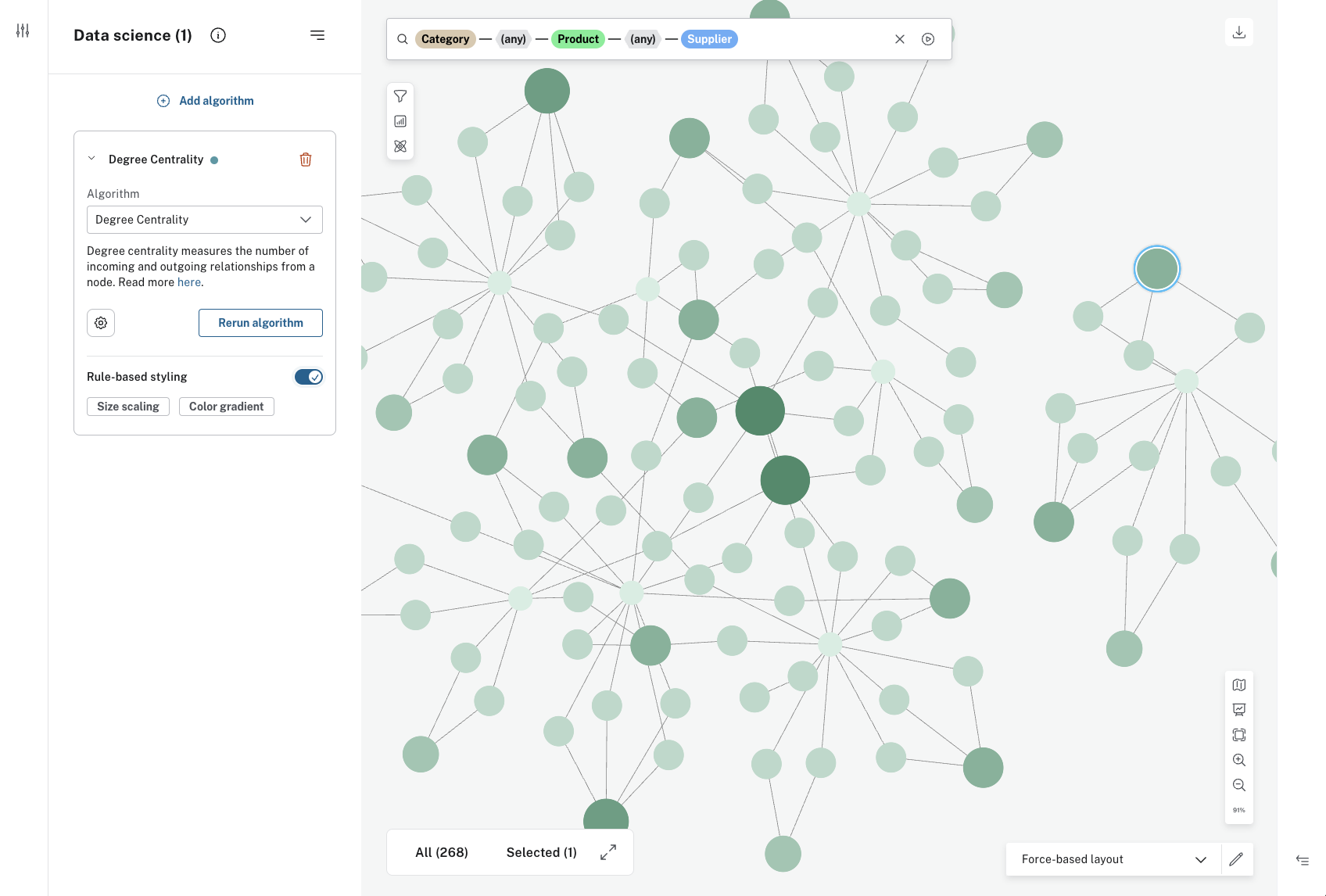
Degree Centrality

The Degree Centrality algorithm measures the relationships connected to a node, either incoming, outgoing, or both, to find the most connected nodes in a graph.

Betweenness Centrality

The Betweenness Centrality algorithm finds influential nodes, that is, nodes that are thoroughfares for the most shortest-paths in the scene. Nodes with a high degree of betweenness centrality are nodes that connect different sub-parts of a graph.

Eigenvector Centrality

The Eigenvector Centrality algorithm is used to measure transitive influence of nodes. That means that for a node to score a high eigenvector centrality, it needs to be connected to other nodes which in turn are well-connected. The difference between the eigenvector and the betweenness centrality is that the eigenvector is not only based on a node’s direct relationships with other nodes, but on the relationships of the related nodes as well.

PageRank

The PageRank alggorithm is a way to measure the relevance of each node in a graph. The relevance of a node is based on how many incoming relationships from other nodes it has and how important the source nodes are.

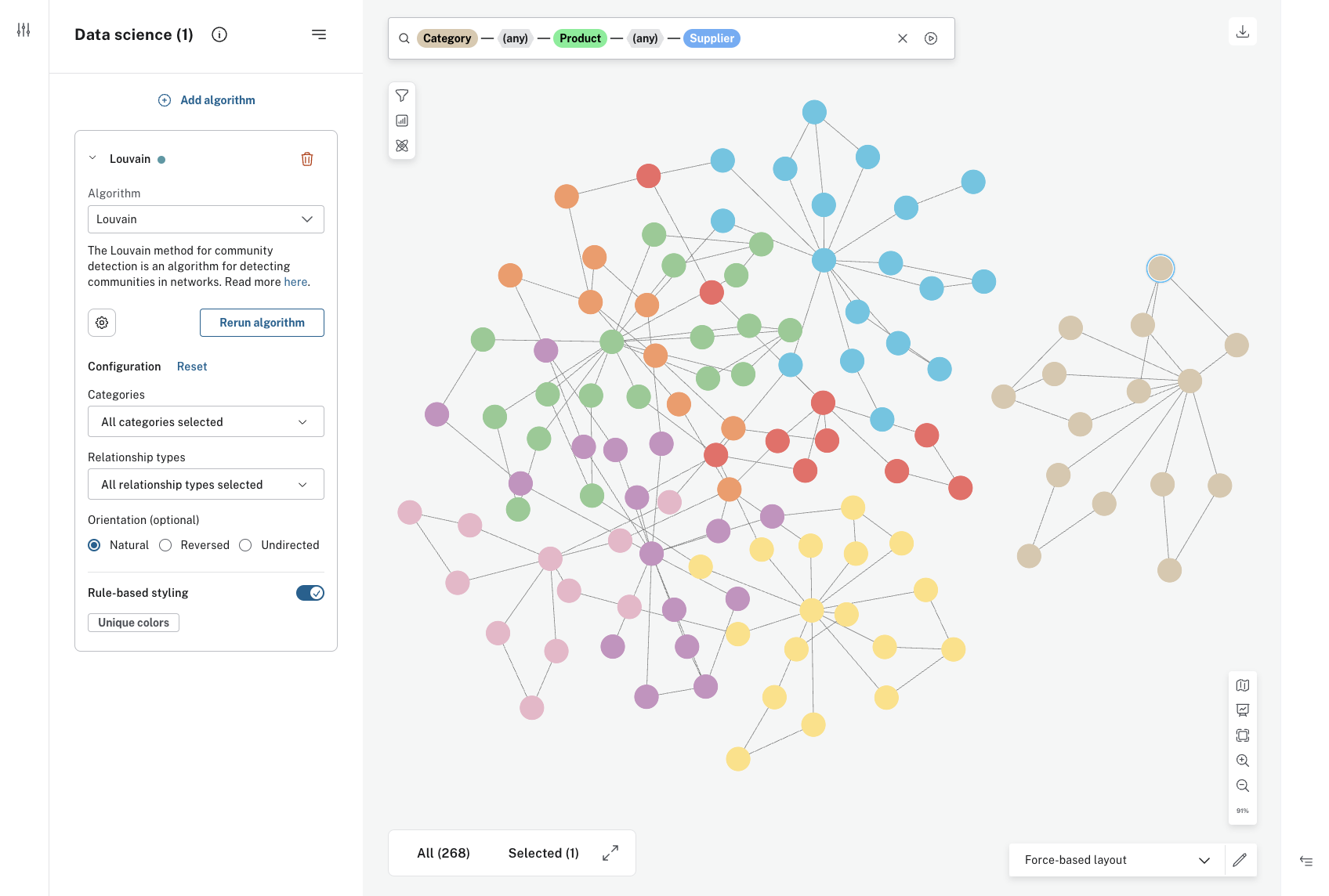
Louvain

The Louvain algorithm aims to find clusters of highly connected nodes within a larger network. It can be useful for product recommendations, for example. If you know a customer bought one product from an identified cluster, they are likely to be interested in another product from that cluster.

Label Propagation

The Label Propagation algorithm is another way to find communities in a graph. One difference between Label Propagation and Louvain, both community detection algorithms, is that this one allows for some supervision, i.e. it is possible to set certain prerequisites that allows for a degree of control of the outcome. This can be useful when you already have some knowledge of the intrinsic structure of your data.

Weakly Connected Components

The Weakly Connected Components algorithm finds subgraphs that are unreachable from other parts of the graph. It can be used to determine whether your network is fully connected or not and also to find vulnerable parts in supply chains, for example.

Using GDS algorithms in Bloom

Prerequisites

To use GDS algorithms in Bloom, there are two things you need to do before you start Bloom:

  • Install the Graph Data Science Library plugin. The easiest way to do this is in Neo4j Desktop. See the Install a plugin section in the Neo4j Desktop manual for more information.

  • Allow GDS in the neo4j.conf file. This can be done manually or via Neo4j Desktop. The dbms.security.procedures.unrestricted setting needs to include both Bloom and GDS (and others that are already specified) as such: dbms.security.procedures.unrestricted=jwt.security.*,bloom.*,gds.*,apoc.*

    The dbms.security.procedures.allowlist setting needs to be uncommented and also needs to include both Bloom and GDS (and others, as mentioned previously) as such: dbms.security.procedures.allowlist=apoc.coll.*,apoc.load.*,gds.*,bloom.*,apoc.*

With these in place, you can start Bloom and start searching to bring some data to your Scene to run the algorithms on.

louvain

Running the algorithms

The GDS algorithms are accessed via the GDS button in the upper-left corner of the Scene. When you have selected an appropriate algorithm, you have the option to run it on all elements in the Scene, or specify which node categories and/or relationship types. Additionally, you can also select the orientation of the relationships to be traversed. The options are accessed via the Settings button in the GDS drawer.

Applying your selected algorithm does not immediately change anything in the Scene. You can inspect each node to see its score, but to make the results easily visible, apply rule-based styling. This is done directly in the GDS drawer. The centrality algorithms are based on a range of values and can be either size-scaled or color gradient, while the community detection algorithms use unique values and offer unique colors to style the nodes.

degree centrality